Determine o conjunto solução da seguinte inequação:
Passo 1
Vamos observar algumas coisas.
Primeiro: Essa função nunca será igual a zero, pois o numerador nunca será igual a zero.
Segundo: Se você prestar atenção, o numerador sempre será positivo, então para essa função ser negativa, o denominador precisa ser negativo.
Ou seja, podemos dizer:
Passo 2
Vamos resolver essa nova inequação agora
Como a base é maior do que 1, podemos escrever:
A raiz de vai ser igual a 0 e a raiz de vai ser igual a 1. As duas são funções do 1º grau CRESCENTES.
Sendo assim, vamos montar a nossa tabelinha.
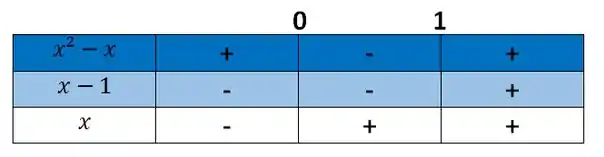
Show?
Então nossa solução será:
Resposta
Exercícios de Livros Relacionados
Demonstrar:Se a = 0 e b = 0 , então a^2 = b^2 se e somente se a = b .