Calcule a integral.
Passo 1
Galera, o exercício quer que a gente calcule uma integral que tem esses numerozinhos em cima e em baixo dela. O que eles são?
Esses numerozinhos são chamados de limites de integração.
Quando uma integral tem esses limites de integração, ela é chamada de integral definida!
Mas relaxa, porque nesse início de resolução a gente não vai usar os limites de integração!
Antes, temos que lembrar que tirar a raiz quadrada é a mesma coisa que elevar a ! Olha só:
Além disso, elevar dois números juntos é a mesma coisa que elevar cada número separadamente!
Substituindo isso na integral, encontramos:
Essa integral está pronta pra ser calculada! No próximo passo a gente vai integrar!
Passo 2
Primeiro, nós temos lembrar que a as constantes não interferem na integral e podem ser tiradas de dentro dela. é uma constante. O fato de ela estar elevada a um número, não muda o fato de ela ser uma constante.
Colocando pra fora da integral, achamos:
Agora só sobrou o elevado a !
Sempre que tivermos elevado a um número, podemos usar uma regrinha.
A regrinha é: soma no expoente e divide por esse resultado. Ou seja, a regrinha geral, ficaria assim:
Para usar essa regra, nós temos que lembrar que o expoente de vale . Logo:
Para fazer essa conta, precisamos reescrever o que está sozinho no mesmo denominador que a fração . Para isso, vamos transformar ele na fração . Podemos fazer isso porque , então não alteramos o valor do e teremos frações com o mesmo denominador pra somar!
Na hora de somar frações, depois de deixar elas com o mesmo valor no denominador, é só somar os números de cima e repetir o de baixo:
Substituindo isso na integral, achamos:
Note que os limites de integração ainda estão presentes para lembrar que eles ainda precisam ser usados. Não vamos usá-los agora, mas é importante deixa-los aí!
Vamos só arrumar melhor nossa resposta.
Quando dividimos um número por uma fração, nós podemos multiplicar a parte de cima pelo inverso da fração. A parte de cima é o . O inverso da fração vale . Com isso, temos que:
Outra coisa que podemos fazer, é reescrever essas potências que tem fração no expoente, em forma de raízes. Pra isso vamos usar a regra abaixo:

Então o
E o
Escrevendo dessa maneira, fica um pouquinho melhor pra entender. E nossa integral se torna:
Agora só falta aprender a usar os limites de integração. No próximo passo a gente faz isso!
Passo 3
Finalmente vamos usar os limites de integração!
Fazemos isso, substituindo o pelos dois limites! Em outras palavras, nós vamos trocar os por um limite de cada vez. Primeiro, nós vamos trocar o pelo limite de cima (pelo ) e depois vamos trocar pelo limite debaixo (pelo ). A regra de troca do é mostrada abaixo.
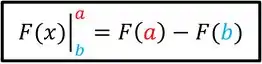
Usando essa regra, a expressão vira:
Nós podemos tirar o termo com da equação pra deixar um pouco mais simples, já que , e como ele está multiplicando o , essa parte inteirinha vai sumir, sobrando só:
Vamos fazer esse cálculo no último passo!
Passo 4
Para resolver essa conta vamos começar pela . Quando existe uma potência dentro da raiz a gente pode jogar ela pra fora da raiz, resolver a raiz só do que sobrou, e depois a gente resolve a potência. Assim ó:
Show, agora a gente encaixa isso no resultado da nossa integral:
Dividindo o por e multiplicando por , vamos ficar com:
Enfim achamos quanto vale a integral do enunciado! Show!