Calcule a integral.
Passo 1
Ixiii, temos um módulo alí na função, mas calma, só precisamos analisar esse módulo e vai dar tudo certo.
Essas barras são chamadas de módulo. O termo da nossa função é lido como: “o módulo de ”.
E o que o módulo faz de diferente?
O módulo é o seguinte: caso o termo que estiver dentro do módulo seja negativo, o módulo o fará ficar positivo. Mas se o termo que está lá dentro já for positivo, o módulo o manterá positivo.
Mas como ele faz isso???? Vamos ver um exemplinho pra dar aquela clareada nas ideias. Para isso vamos usar outro valor qualquer, tipo o 5:
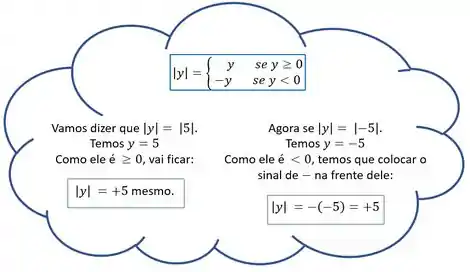
No nosso balazinho, o foi multiplicado por pra ficar positivo, por isso colocamos esse menos na frente dele.
Agora vamos ver como fica para o nosso exercício.
No nosso caso, o termo que está dentro do módulo é o . E saberemos que ele é negativo se ele for menor que zero.
Veja bem, para a nossa integral, como o intervalo de integração vai de a , e a função dentro do módulo é a função seno, olhando para o gráfico dela podemos ver que tem um pedaço dela que é positivo e outro que é negativo. O que teremos que fazer então, é dividir nossa integral em dois pedaços.
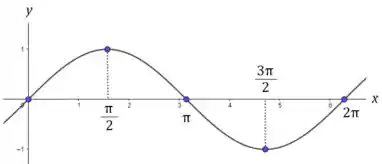
Veja como em a função deixa de ser positiva (ficar acima do eixo x) e passa a ser negativa (abaixo do eixo x). Faremos então o intervalo de integração de a temos que a função seno é positiva, então usamos , já no intervalo de a a função seno é negativa, assim (colocamos o menos na frente, por causa do lance do módulo), e vai ficar assim:
Viu? Agora fica simples de resolver, vamos lá!
Passo 2
Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Agora vamos achar as primitivas de cada função, usando duas expressões da Tabela de Integrais Indefinidas:
Agora é só aplicar, vamos resolver elas separadamente, assim fica mais simples de ver:
Para podemos colocar o do lado de fora da integral:
Passo 3
Pronto, já encontramos a integral indefinida, perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Ficamos então com:
Aaahhh, aqui não podemos cancelar o ) com o porque os limites de integração não diferentes tá!