Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Triplas

Ver Teoria
Exercício 61234578910

Enunciado

Calcule a integral, mudando a ordem de integração de forma apropriada

∫ 0 1 ∫ 0 1 ∫ x 2 1 12 x z   e z y 2 d y d x d z

Passo 1

Olaaa, vamos continuar com nosso estudo das integrais triplas!

Assim como aconteceu no exemplo da teoria, vemos que não conseguiríamos integrar direto em função de y . Portanto, vamos ter que integrar alguma outra variável antes, certo? Fazendo uma mudança na ordem de integração.

Vamos antes entender o nosso sólido, pelos limites da integral, temos que:

0 ≤ x ≤ 1

x 2 ≤ y ≤ 1

0 ≤ z ≤ 1

Esboçando esses limites temos:

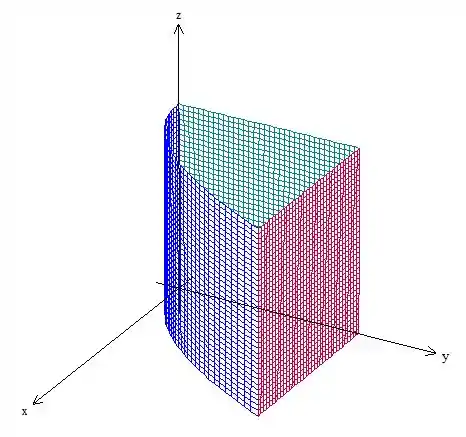
Passo 2

Como não queremos integrar em y , vamos mudar a ordem de integração para d x d y d z

No plano x y , tínhamos y limitado por

y = x 2

y = 1

E x limitado por

x = 0

x = 1

No plano x y , ficamos com: (se tiver dificuldade, é só imaginar você olhando esse sólido por cima 😊)

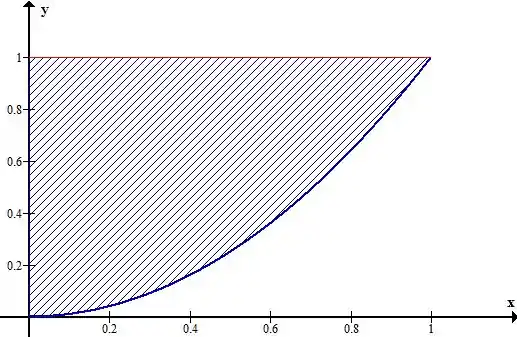
Agora, vamos pro que interessa hehe, invertendo a ordem de integração:

y = x 2  

Tirando a raiz dos dois lados, ficamos com

x = ± y

Como temos que x é positivo, vamos pegar somente a raiz positiva, então temos que:

0 ≤ x ≤ y

E, pelo gráfico conseguimos ver que:

0 ≤ y ≤ 1

E os limites de z continuam os mesmos:

0 ≤ z ≤ 1

Passo 3

Reescrevendo a integral, ficamos com:

∫ 0 1 ∫ 0 1 ∫ 0 y 12 x z e z y 2 d x d y d z

Passo 4

Show, conseguimos fugir de y por enquanto haha, então vamos integrar em x :

∫ 0 1 ∫ 0 1 ∫ 0 y 12 x z e z y 2 d x d y d z

Então vamos focar nessa parte

∫ 0 y 12 x z e z y 2 d x

Como estamos integrando em relação a x , podemos colocar tudo que não é x para fora da integral, ficando com

12 z e z y 2 ∫ 0 y x d x

Agora ficou mais tranquilinho né?

12 z e z y 2 ⋅ x 2 2 0 y

Substituindo isso ficamos com

12 z e z y 2 ⋅ y 2 - 0 2 2

Resolvendo isso temos

6 z e z y 2 y

Passo 5

Vamos pegara essa integral e colocar nas integrais de fora

∫ 0 1 ∫ 0 1 6 y z e z y 2 d y d z

Olhando só em relação a y , temos

∫ 0 1 6 y z e z y 2 d y

Agooooora a gente pode resolver isso ai, percebe que o y que ta embaixo é bem parecido com a derivada de y 2 ? hehe, então vamos ter

Para integrar em y , vamos fazer a substituição simples

y 2 = u

2 y d y = d u

d y = d u 2 y

Os limites em u ficam:

y 2 = u

Quando y = 0 , temos:

u = 0 2 = 0

Quando y = 1 , temos:

u = 1 2 = 1

Temos então a integral em relação a u fica

∫ 0 1 6 y z e z u d u 2 y

Simplificando, temos

∫ 0 1 3 z e z u d u

Agora resolvendo essa integral temos:

3 e z u | 0 1

Substituindo isso, temos

3 e z - e 0

Como e 0 = 1 , temos

3 ( e z - 1 )

Passo 6

Podemos pegar esse resultado e aplicar na nossa última integral, (ufa)

Integrando em u :

3 ∫ 0 1 e z - 1 d z

Integrando em z , temos:

3 e z - z z = 0 z = 1

Substituindo os valores, temos

3 e - 1 - e 0 - 0 =

3 e - 2 = 3 e - 6  

Resposta

3 e - 6

Exercícios de Livros Relacionados

a) Resolva o sistema u = 3x + 2y, v = x + 4y , para x e y em termos de u e v. Em seguida, encontre o valor do jacobiano ∂(x, y)/∂(u, v).b) Encontre a imagem pela transformação u = 3x + 2y, v = x +4y d
Calcule as integrais nos Exercícios 7-20.int_1^e int_1^(e^2) int_1^(e^3) (1)/(x y z) d x d y d z
Calcule as integrais nos Exercícios 7-20.int_0^1 int_0^1 int_0^1 (x^2 + y^2 + z^2) d z d y d x
Calcule as integrais nos Exercícios 7-20.int_0^((pi)/(6)) int_0^1 int_(- 2)^3 y s e n (z) d x d y d z
Calcule a integral ∫ 0 4 ∫ x = y 2 x = y 2 + 1 2 x - y 2 d x d y do Exemplo 1 diretamente pela integracao com relacao a x e y para confirmar que seu valor e 2.