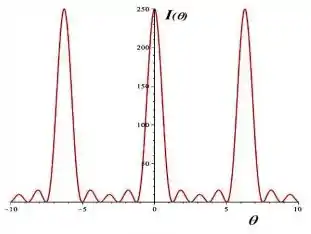
Considere uma onda incidindo sobre um dispositivo de interferência com N fendas. O comprimento de onda é λ. A figura ao lado é o gráfico da intensidade I(θ) versus o ângulo θ detectado na tela de observação. Esse ângulo é dado em graus e a intensidade máxima vale 250xW/.

Determine o número de fendas,

A intensidade da onda em uma fenda(I0)

e a distância d entre as fendas em função de λ.

O numero de máximos secundários, que são os máximos entre dois máximos principais, é dado pela Fórmula

Em que é o numero de máximos secundários e é o numero de fendas em que o nosso raio luminoso incide.

Também devemos lembrar que o valor da intensidade máxima também se relaciona com o numero de fendas, pela fórmula

Em que é a intensidade máxima do feixe e é a intensidade inicial do feixe.

E por fim devemos relembrar a fórmula que possui o comprimento de onda. Essa fórmula nos da as condições de mínimo do nosso gráfico, ou seja, de franjas escuras, em que a relação é

Em que

sabendo agora com cada fórmula funciona vamos analisar o nosso exercício

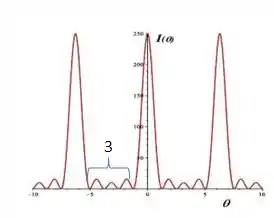
Pelo gráfico temos que o numero de máximos secundários entre dois máximos principais é 3 com vemos na figura

Substituindo na fórmula teremos

Logo o numero de fendas é 5

Com o numero de fendas conseguimos facilmente determinar o valor de , já que temos o valor de no gráfico.

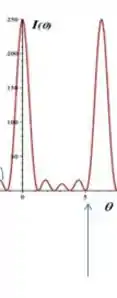
Por fim, vemos pelo gráfico que sobre o ângulo de 5° temos um 4º mínimo ocorrendo, e lembre-se, só usamos esse valor pois é o único que o exercício nos dá, se ele tivesse dado o ângulo do primeiro mínimo não seria necessário usar o quarto, mas aqui trabalhamos com o que o exercício da, então tem que ser o quarto mínimo.

como o objetivo do exercício é determinar a distância entre as fendas em função do comprimento de onda teremos