Em uma demonstração de interferência com ondas sonoras, cinco alto-falantes emitem ondas de frequência igual a e intensidade .
Os alto-falantes estão em fase e separados entre si por uma distância de . A disposição geométrica dos alto-falantes é mostrada na figura abaixo.
As medidas da intensidade do som são feitas por um experimentador que se posiciona sobre a reta , a do plano que contém os alto-falantes. A velocidade do som no ar nas CNTP é de .
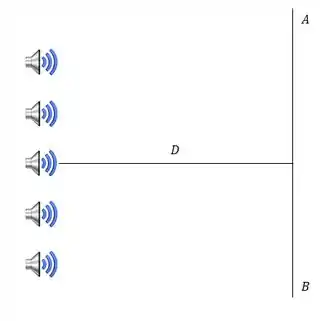
Considere os alto-falantes como fontes puntiformes, e despreze efeitos de reflexão nas paredes do laboratório.
- Calcule o valor máximo da razão , onde é a intensidade de um alto-falante.
- Calcule a distância linear sobre a reta de observação entre o máximo central e um máximo principal de primeira ordem.
- Quantos zeros há entre dois máximos principais consecutivos?
- Faça o diagrama de fasores correspondente ao primeiro mínimo.
Passo 1
Letra (a): Calcule o valor máximo da razão , onde é a intensidade de um alto-falante.
Para mais de múltiplas fendas, a interferência é dada por:
Onde é o número de fendas e, no nosso caso, o número alto-falantes.
Uma das informações muito importantes que podemos tirar dos gráficos é que a altura de cada máximo principal é proporcional a .
Como temos 5 fendas, o gráfico da interferência é algo desse tipo:
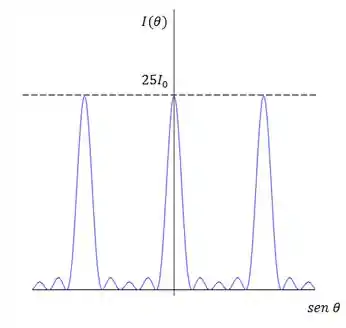
Assim, o maior valor possível da fração será referente ao maior valor possível de , que, caso de 5 fendas, será:
Logo:
Passo 2
Letra (b): Calcule a distância linear sobre a reta de observação entre o máximo central e um máximo principal de primeira ordem.
O problema nos pede a distância linear sobre a reta de observação .
Os máximos maiores estão localizados nas mesmas posições do caso de fenda dupla.
Logo, a posição dos máximos, medida a partir do máximo central é dada por:
Onde:
;
;
Como o problema está falando do máximo principal de primeira ordem,
Nos falta apenas descobrir o valor de .
Passo 3
Como o problema nos dá a frequência e a velocidade da onda, para descobrir o valor do comprimento de onda , podemos usar a seguinte relação:
Onde:
;
;
Logo:
Passo 4
Passo 5
Letra (c): Quantos zeros há entre dois máximos principais consecutivos?
Para fendas, outra informação muito importante que podemos tirar dos gráficos é que entre dois máximos principais existem máximos secundários e mínimos, respondendo a nossa pergunta.
Assim, existem zeros entre dois máximos principais.
Passo 6
Letra (d): Faça o diagrama de fasores correspondente ao primeiro mínimo.
Cada um dos mínimos ocorre quando a diferença de fase entre duas ondas consecutivas é dada por:
Como estamos falando do primeiro mínimo, a diferença de fase é dada por:
Passo 7
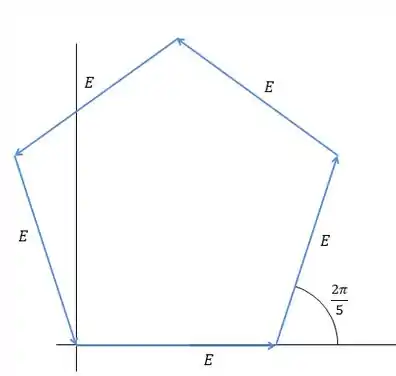
Como se tratam de 5 fendas, o diagrama de fasores será desta forma.
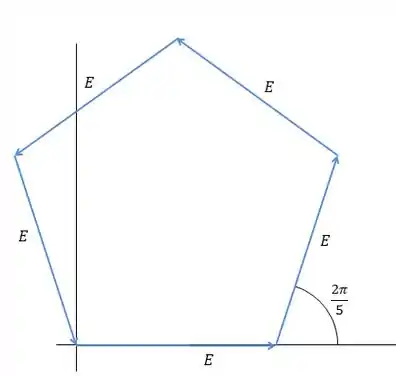
Resposta
Letra (a):
Letra (b):
Letra (c):
Existem 4 zeros entre dois máximos principais.
Letra (d):