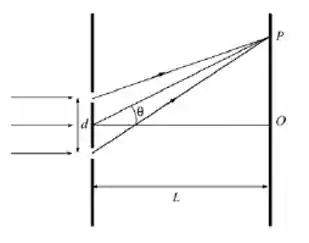
Em um experimento de Young, a separação entre as fendas é muito maior do que a largura delas. A luz que parte das fendas incide sobre um anteparo localizado a uma distância , paralelo ao plano das fendas e , conforme a figura.
A luz incidente possui dois comprimentos de onda e . São observados dois padrões de interferência no anteparo, cada um deles correspondendo a um comprimento de onda.
Para , os máximos de interferência de e se sobrepõem. Qual é o menor valor de para o qual os máximos de e vão se sobrepor novamente?
Passo 1
Como a separação entre as fendas é muito maior que a largura delas, podemos considerá-las como sendo pontuais.
Assim, a posição das franjas brilhantes pra cada comprimento de onda vai ser:
Essas franjas vão se sobrepor quando:
Como e , temos:
Ou, de outra forma:
Como é um número inteiro, isso significa que também deve ser inteiro, o que só é possível se for um múltiplo de 4.
Assim, os máximos que vão se sobrepor vão ser:
E por aí vai...
Passo 2
O menor ângulo onde as franjas vão se sobrepôr corresponde às menores ordens (menores e ). Assim, podemos usar qualquer uma das duas condições de máximo para achar o ângulo.
Usarei , e nesse caso teremos de usar e o enunciado diz que
Invertendo a função seno temos:
O que corresponde à letra a).
Resposta
Letra a)