(Adaptada) Considere o problema de condução unidimensional numa parede plana de largura e altura , com uma extremidade isolada e a outra mantida a temperatura igual a .
A parede tem condutividade térmica igual a , e no seu interior passa uma resistência elétrica que gera calor uniformemente a uma taxa de .
Escreva a equação de condução de calor e as condições de contorno apropriadas para essa situação. Em seguida, obtenha a distribuição de temperatura ao longo da parede e desenhe um gráfico (qualitativo) da temperatura x distância para a situação analisada.
Passo 1
A equação de calor é dada por:
Sabendo que a condução é unidimensional e supondo regime permanente, teremos:
Além disso, supondo que as propriedades do material sejam as mesmas em qualquer ponto da placa, teremos:
O problema nos disse que uma extremidade da placa é isolada termicamente, e a outra mantida a temperatura igual a .
Assim, as condições de contorno serão:
Passo 2
Resolvendo a equação diferencial que encontramos, teremos:
Integrando a equação em :
Aplicando a condição de contorno de superfície isolada termicamente, teremos:
Integrando novamente em :
Aplicando a condição de contorno de temperatura constante:
Assim, a distribuição de temperatura será dada por:
Passo 3
Pra analisar esse perfil de forma qualitativa, vamos dar uma olhada na função que descreve a temperatura. A temperatura é uma função de segundo grau em relação a , então será uma parábola. Como o termo do é negativo, a concavidade é para baixo.
Podemos fazer uma análise mais quantitativa, já que sabemos que, em , na extremidade da parede, .
Um esboço de versus pode ser feito assim:
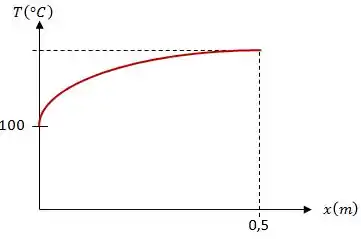
Resposta
Equação de calor:
Distribuição de temperatura: