Uma panela é usada para ferver água. Ela é colocada sobre um fogão, a partir do qual calor é transferido a uma taxa fixa . Há dois estágios no processo.
No Estágio 1, a água é levada de sua temperatura inicial (ambiente) até o ponto de ebulição, quando calor é transferido da panela para a água por convecção natural. Durante esse estágio pode-se admitir um valor constante do coeficiente de transferência de calor , enquanto a temperatura média da água aumenta com o tempo,
No Estágio 2, a água encontra-se em ebulição e a sua temperatura mantém-se em um valor fixo, , enquanto o fornecimento de calor continua.
Considere uma base de panela com espessura e diâmetro , com um sistema de coordenadas no qual e nas superfícies em contato com o fogão e com a água, respectivamente.
Escreva a forma da equação do calor e as condições inicial e de contorno que determinam a variação da temperatura com a posição e o tempo, , na base da panela ao longo do Estágio 1. Expresse o seu resultado em termos dos parâmetros , , , e , assim como das propriedades pertinentes do material da panela.
Durante o Estágio 2 a superfície da panela em contato com a água encontra-se a uma temperatura fixa, . Escreva a forma da equação do calor e as condições de contorno que determinam a distribuição de temperaturas, , na base da panela. Expresse o seu resultado em termos dos parâmetros , , e , assim como das propriedades pertinentes do material da panela.
Passo 1
Vamos nessa, meu time! A ideia aqui é essa:
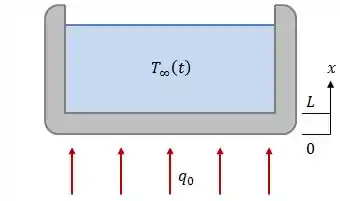
Ou seja, nos dois Estágios teremos uma taxa de transferência de calor na superfície . A única coisa que vai mudar será a condição de contorno para , que é a superfície que está em contato com a água.
Um detalhe importante aqui é que o problema nos dá a taxa de transferência de calor mas, na hora de aplicar as condições de contorno, vamos trabalhar com o fluxo de calor. Para isso, basta usar a relação:
Como o problema nos deu o diâmetro da base da panela, podemos escrever que:
Logo:
Show de bola! Agora vamos analisar cada um dos estágios, beleza?
Passo 2
Escreva a forma da equação do calor e as condições inicial e de contorno que determinam a variação da temperatura com a posição e o tempo, , na base da panela ao longo do Estágio 1. Expresse o seu resultado em termos dos parâmetros , , , e , assim como das propriedades pertinentes do material da panela.
Estágio 1
Considerações:
- Transferência de calor somente no eixo ;
- Não há geração de calor interna;
- Propriedades do material constantes;
- Fluxo de calor constante na superfície ;
- Convecção na superfície ;
- Temperatura inicial .
Começando pela Equação do Calor, temos que:
Aplicando as nossas considerações, teremos o seguinte:
Onde .
Em , temos uma condição de fluxo de calor constante, logo:
Em , temos uma condição de convecção na superfície, logo:
Pra fechar, não podemos esquecer que, inicialmente, todo o sistema está a temperatura ambiente. Sendo assim:
Pronto! Nem doeu! ;)
Vamos pro Estágio 2.
Passo 3
Durante o Estágio 2 a superfície da panela em contato com a água encontra-se a uma temperatura fixa, . Escreva a forma da equação do calor e as condições de contorno que determinam a distribuição de temperaturas, , na base da panela. Expresse o seu resultado em termos dos parâmetros , , e , assim como das propriedades pertinentes do material da panela.
Estágio 2
Considerações:
- Transferência de calor somente no eixo ;
- Não há geração de calor interna;
- Propriedades do material constantes;
- Fluxo de calor constante na superfície ;
- Temperatura constante em .
Começando pela Equação do Calor, é importante ressaltar que, como agora a temperatura está constante em , não há mais variação de temperatura com o tempo, já que a água está passando por mudança de fase, dessa forma:
Aplicando as nossas considerações, teremos o seguinte:
Em , temos uma condição de fluxo de calor constante, logo:
Em , temos uma condição de temperatura constante, logo:
Acabou! :)
Resposta