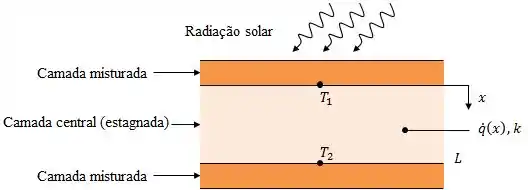
Um tanque solar de gradiente salino é um corpo raso de água, composto por três camadas distintas de fluidos, que é usado para coletar energia solar.
As camadas externas superior e inferior encontram-se bem misturadas e servem para manter as superfícies superior e inferior da camada intermediária em temperaturas uniformes e , onde . Embora exista movimentação do fluido nas camadas misturadas, tal movimento não está presente na camada central.
Considere condições nas quais a absorção de radiação solar na camada central implique em geração de calor não-uniforme na forma e a distribuição de temperaturas nessa camada seja:
As grandezas , , e são constantes conhecidas que possuem as unidades indicadas e é a condutividade térmica, que também é constante.
Obtenha expressões para a taxa, por unidade de área, na qual o calor é transferido da camada inferior misturada para a camada central e da camada central para a camada superior misturada.
Determine se as condições do sistema são de regime estacionário ou de regime transiente.
Obtenha uma expressão para a taxa na qual a energia térmica é gerada em toda camada central, por unidade de área superficial.
Passo 1
Obtenha expressões para a taxa, por unidade de área, na qual o calor é transferido da camada inferior misturada para a camada central e da camada central para a camada superior misturada.
Quando o problema pede a taxa por unidade de área, ele está tentando dizer educadamente que quer que a gente determine a bagaça do fluxo de calor, show?
Graficamente, como , a ideia é a seguinte:
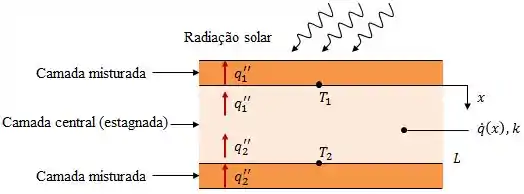
Se o problema já nos disse como a temperatura varia com o valor de , podemos começar calculando o fluxo de calor por condução:
Agora basta calcular o fluxo de calor nas duas superfícies e acabou o problema (pelo menos essa parte):
Passo 2
Determine se as condições do sistema são de regime estacionário ou de regime transiente.
Para resolver o problema, precisamos analisar a Equação do Calor e observar se:
- : Regime estacionário;
- : Regime transiente.
Vamos lá:
Aqui, vamos fazer as seguintes considerações:
- Transferência de calor somente na direção ;
- Condutividade térmica constante.
Aplicando essas condições na Equação do Calor (onde ), teremos:
O último trabalho que teremos aqui é calcular a segunda derivada :
Substituindo na expressão na Equação do Calor, teremos:
Dessa forma, as condições do sistema são de regime estacionário.
Passo 3
Obtenha uma expressão para a taxa na qual a energia térmica é gerada em toda camada central, por unidade de área superficial.
Novamente, como o problema está pedindo a taxa de energia térmica por unidade de área, o que ele quer que a gente calcule é o fluxo de energia térmica gerada. Este fluxo de energia pode ser calculado da seguinte forma:
Substituindo a expressão de , teremos:
Arrumando a casa, teremos o seguinte:

Resposta
As condições do sistema são de regime estacionário.