Considere condições de regime estacionário na condução unidimensional em uma parede plana com uma condutividade térmica de e uma espessura , sem geração interna de calor.

Determine o fluxo térmico e a grandeza desconhecida em cada caso e esboce a distribuição de temperaturas, indicando a direção do fluxo térmico.
Passo 1
Vamos nessa! De acordo com o problema, vamos trabalhar com o fluxo de calor por condução , dado por:
Como estamos trabalhando com a diferença de temperatura através de uma parede plana, podemos dizer que:
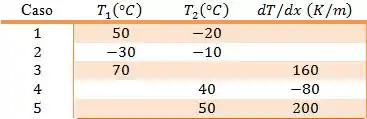
Se liga! Na tabela, temos que colocar como , mas o problema nos deu as temperaturas em ... como fazemos então?!
Calma! Por conta da relação entre temperaturas em Kelvin e Celsius , a variação de temperatura terá o mesmo valor, seja em graus, ou em Celsius! Então não precisamos esquentar a cabeça com isso, ok?
Além disso, teremos que determinar o sentido do fluxo térmico pra cada caso. Aqui, é importante lembrar que o fluxo térmico flui do ponto de maior temperatura para o ponto de menor temperatura.
Bom, esses conhecimentos são o suficiente pra resolver o problema. Vamos analisar, então, um caso por vez, beleza?
Passo 2
Caso 1:
Dados:
Vamos começar calculando a grandeza que falta na tabela, e depois usá-la pra calcular o fluxo de calor.
Agora estamos prontos pra calcular o fluxo de calor, dado por:
Como , o fluxo térmico vai para a direita.
Passo 3
Caso 2:
Dados:
Mesmo esquema aqui, vamos começar calculando para depois calcular o fluxo de calor, ok?
Como , o fluxo térmico fluirá para a esquerda.
Passo 4
Caso 3:
Dados:
Como o problema já nos deu , podemos calcular o fluxo de calor sem maiores problemas:
Para calcular , vamos fazer utilizar a seguinte relação:
Opa! Podemos reorganizar essa equação para encontrar :
Como , o fluxo térmico vai para a esquerda.
Passo 5
Caso 4:
Dados:
Novamente, como o problema já nos deu , podemos calcular logo o fluxo de calor:
Para calcular , vamos reorganizar a equação abaixo:
Como , o fluxo térmico fluirá para a direita.
Passo 6
Caso 5:
Dados:
Mesmo esquema do passo anterior, vamos começar calculando o fluxo de calor:
Para calcular , vamos reorganizar a equação abaixo:
Como , o fluxo térmico vai para a esquerda.
Resposta
- Caso 1:
- Caso 2:
- Caso 3:
- Caso 4:
- Caso 5:
O fluxo térmico vai para a direita.
O fluxo térmico vai para a esquerda.
O fluxo térmico vai para a esquerda.
O fluxo térmico vai para a direita.
O fluxo térmico vai para a esquerda.