Água a uma temperatura de escoa sobre uma das superfícies de uma parede de aço (AISI 1010), cuja temperatura de . A parede possui uma espessura de e sua outra superfície está a uma temperatura de .
Para condições de regime estacionário, qual é o coeficiente convectivo associado ao escoamento da água?
Quais são os gradientes de temperatura na parede e na água que está em contato com a parede?
Esboce a distribuição de temperaturas na parede e na água a ela adjacente.
Passo 1
Antes de qualquer coisa, precisamos das propriedades de cada material envolvido no problema.
Para o aço (AISI 1010), as propriedades serão tomadas na temperatura média entre as superfícies:
De acordo com a tabela A.1 do Incropera (fazendo uma interpolação linear), encontramos que .
Para a água, vamos buscar as propriedades de acordo com a temperatura média entre a de escoamento livre e a da placa em contato com o fluido. Logo:
De acordo com a tabela A.6 do Incropera .
Agora podemos seguir em frente.
Passo 2
Para condições de regime estacionário, qual é o coeficiente convectivo associado ao escoamento da água?
A ideia do problema é essa aqui:
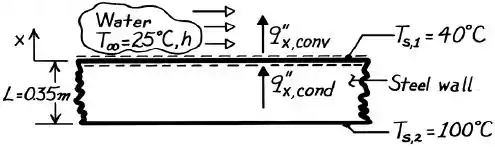
Como estamos trabalhando com regime permanente, o fluxo de calor por condução que chega à superfície de deve ser igual ao fluxo de calor por convecção que é transferido da mesma para a água. Logo:
Reorganizando os termos:
Substituindo os valores:
Passo 3
Quais são os gradientes de temperatura na parede e na água que está em contato com a parede?
Quando falamos em gradiente de temperatura, estamos falando na Lei de Fourier, logo, para a parede:
Já para a água em contato com a parede, temos que:
Passo 4
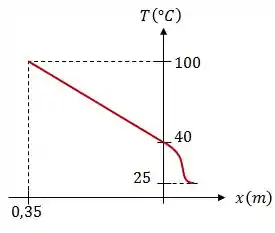
Esboce a distribuição de temperaturas na parede e na água a ela adjacente.
A temperatura varia linearmente no interior do aço mas quando passa para o fluido, a temperatura se comporta de maneira diferente, assim, como vimos na Teoria. Logo, a distribuição de temperatura vai ter essa cara:
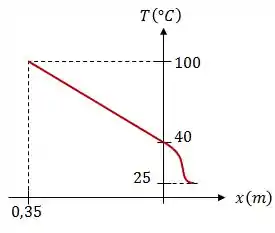
Resposta