Ar com uma temperatura na corrente livre de , escoa paralelamente sobre uma placa plana de comprimento e temperatura .
Entretanto, obstáculos colocados no escoamento intensificam a mistura com o aumento da distância da aresta frontal e a variação espacial das temperaturas medidas no interior da camada-limite é correlacionada por uma expressão da forma onde e representam respectivamente os eixos horizontal e vertical, e estão em metros.
Determine e represente graficamente a maneira pela qual o coeficiente convectivo local varia com . Calcule o coeficiente convectivo médio para a placa.
Passo 1
Por definição, o coeficiente convectivo é dado por:
Opa! Antes de continuarmos precisamos saber quanto vale a condutividade térmica do ar nessas condições.
Para pegar o valor de , utilizaremos a temperatura média entre a de corrente livre e a da superfície da placa .
De acordo com a tabela A.4 do Incropera (e fazendo uma interpolação linear), encontramos que .
Passo 2
Voltando para a expressão de :
Onde:
Temos que:
Passo 3
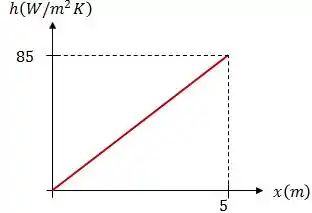
Graficamente, o coeficiente convectivo irá variar linearmente com , de acordo com a função que encontramos no passo anterior.
Para (aresta traseira da placa), . Dessa forma:
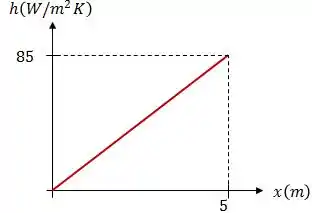
Passo 4
Pra fechar, temos que calcular o coeficiente convectivo médio. Pra isso, como o mesmo varia somente com , basta utilizar a expressão:
Substituindo os limites de integração:
Onde , logo:
Resposta