A taxa de transferência de calor, por unidade de largura (normal à página), em uma seção longitudinal,, , pode ser representada por , onde é o coeficiente médio na seção de comprimento .
Considere escoamento laminar sobre uma placa plana com uma temperatura uniforme . A variação espacial do coeficiente convectivo local tem a forma , onde é uma constante.
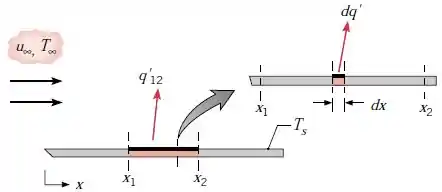
Partindo da equação da taxa convectiva na forma , deduza uma expressão para em termos de , e .
Deduza uma expressão para em termos de , e dos coeficientes médios e , correspondentes aos comprimentos e respectivamente.
Passo 1
Partindo da equação da taxa convectiva na forma , deduza uma expressão para em termos de , e .
Beleza, temos que partir dessa equação aqui:
Se integrarmos esse cara entre os pontos e (que estamos interessados), encontraremos o seguinte:
Ao mesmo tempo, o próprio enunciado, como quem não quer nada, nos disse que:
Opa! Se igualarmos essas duas expressões, teremos que:
Reorganizando os termos:
No próximo passo, vamos partir pra integração desse cara.
Passo 2
Segundo o enunciado, . Substituindo isso na expressão de :
Agora é só integrar e arrumar a casa:
Finalmente:
Passo 3
Deduza uma expressão para em termos de , e dos coeficientes médios e , correspondentes aos comprimentos e respectivamente.
Então, nós podemos resolver essa questão de duas formas: calcular , e relacioná-los com , ou utilizar a própria o conceito da taxa de transferência de calor dada pelo problema.
Os coeficientes médios e serão dados por:
Agora o nosso objetivo é encaixar esses dois caras na expressão de que encontramos no passo anterior.
Pra isso, vamos isolar as raízes em cada expressão, ok?
Substituindo na expressão de , teremos:
Organizando a bagunça, teremos que:
Resposta