Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Convecção

Ver Teoria
Exercício 51234

Enunciado

O escoamento paralelo de ar atmosférico sobre a superfície de uma placa plana de comprimento L = 3   m é perturbado por uma série de bastões estacionários posicionados na trajetória do escoamento sobre a placa.

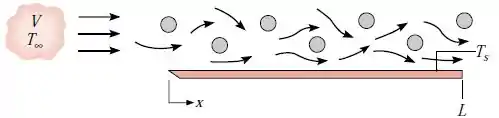
Medidas em laboratório do coeficiente convectivo local na superfície da placa foram efetuadas para um dado valor de V e T s > T ∞ . Os resultados são correlacionados por uma expressão na forma h x = 0,7 + 13,6 x - 3,4 x 2 , onde h x possui unidades de W / m 2 K e x está em metros.

Calcule o coeficiente convectivo médio sobre toda a placa e a razão h L - / h L na aresta traseira x = L .

Passo 1

Por definição, como h x varia somente com x , o coeficiente convectivo médio de toda a placa será dado por:

h L - = 1 L ∫ 0 L h x   d x

Substituindo a expressão de h x :

h L - = 1 L ∫ 0 L 0,7 + 13,6 x - 3,4 x 2   d x

Integrando a expressão acima:

h L - = 1 L 0,7 x + 13,6 x 2 2 - 3,4 x 3 3 0 L

Substituindo os limites de integração:

h L - = 1 L 0,7 L + 6,8 L 2 - 1,13 L 3

h L - = 0,7 + 6,8 L - 1,13 L 2

Onde L = 3   m , logo:

h L - = 0,7 + 6,8 × 3 - 1,13 × 3 2

h L - = 10,9   W / m 2 K

Passo 2

O coeficiente convectivo local aresta traseira x = L será dado por:

h L = 0,7 + 13,6 L - 3,4 L 2

Onde L = 3   m , logo:

h L = 0,7 + 13,6 × 3 - 3,4 × 3 2

h L = 10,9   W / m 2 K

Passo 3

Finalmente, calculando a razão h L - / h L :

h L - h L = 10,9 10,9

h L - h L = 1

Opa! “Então quer dizer que esses caras serão sempre iguais?!”

NÃAAAAAO! Foi só uma coincidência desse problema, ok?! :)

Resposta

h L - h L = 1

Exercícios de Livros Relacionados

Determine a força de arrasto exercida na superfície superior da placa plana do Exemplo 6.4 para temperaturas da água de 300K e 350K . Considere que a dimensão da placa na direção z seja W = 1m .
Uma placa plana fina, com 0,2m × 0,2m de lado, e superfícies superior e inferior rugosas, encontra-se posicionada em um túnel de vento de tal forma que suas superfícies estão paralelas a uma corrente
Como um meio para evitar a formação de gelo nas asas de um pequeno avião particular, propõe-se que sejam instalados elementos aquecedores de resistência elétrica no interior das asas. Para determinar
No escoamento sobre uma placa plana que possui uma superfície muito rugosa, sabe-se que os efeitos da transferência de calor por convecção são correlacionados pela expressão apresentada no Problema 6.
Uma placa delgada e plana, de 0,2m × 0,2m , está orientada paralelamente a uma corrente de ar atmosférico, que possui uma velocidade de 40m / s . O ar está a uma temperatura T ∞ = 20 ° C , enquanto a