Determine o seguinte limite:
Passo 1
Fala aiiii, tudo bem? Estamos começando agora nosso estudo de limites e pode ser que seja uma matéria completamente nova pra você, mas fica tranquilo que vamos começar formando uma base bem legal pra você entender tudinho e nunca mais ter problemas com essa matéria.

Bom, antes de resolvermos a nossa questão, vamos tentar interpretar o que o enunciado está dizendo. Ok? O problema diz pra calcular:
O que esse limite está querendo saber é: De que valor a função ) se aproxima quando fazemos se ficar cada vez mais perto do 2. Ou seja, dizemos que o tende a 2, e é isso que significa aquele embaixo do limite.
Passo 2
Você não precisa desenhar essa função pra calcular o limite, mas deixa eu te mostrar uma coisa que pode clarear nossas ideias. Vamos ver o gráfico dela:
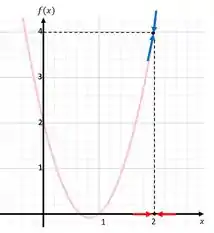
Repare que quando a gente olha para o eixo e vai se aproximando do , que está indicado pela setas vermelhas, a nossa função vai também se aproximando de uma valor , indicado pelas setas azuis.
Pois bem, é isso que o limite que saber da gente. Para que valor caminha a nossa função quando a gente aproxima o valor de a um número de nosso interesse. Dizemos, no nosso caso que o limite da função é igual a quando o .
Mas a gente viu isso pelo gráfico, e não é sempre que dá pra desenhar o gráfico das funções, certo. Então, agora que a gente já sabe o que significa esse limite, vamos ver como resolver de um jeitinho mais direto.
Passo 3
Para resolver esse limite, o que nós fazermos primeiramente é observar que a função é composta por três termos, que são essas parcelinhas ali, o , o e o .
Quando isso acontecer, nós poderemos usar uma propriedade dos limites que diz que a gente pode calcular os limites de cada termo separadamente e depois juntar todo mundo. Ou seja, vamos transformar nosso limite em:
Outra coisa que a gente também pode fazer é usar outra propriedade que diz que quando houver uma constante (um número) multiplicando a função, nós podemos colocá-la pra fora do limite, multiplicando na frente dele. Com isso, podemos tirar o no primeiro limite, e o no segundo. E vai ficar assim:
No último a gente não mexeu, porque só tem o lá. Vamos olhar pra ele com calma logo mais.
Passo 4
Passo 5
Agora que já está tudo arrumado, chegou a hora de calcularmos de fato os nossos limites. E nós faremos isso, substituindo o valor de por em cada um do termos. Isso mesmo, substituindo. Vamos lá:
Nós tiramos o operador e trocamos o por em cada termo, ficando com:
Reparou que no último não tinha o pra substituir. Nesse caso, fica o próprio valor mesmo que já estava lá.
Agora é só resolver essa expressão e ver o que encontramos. Lembrando de fazer primeiro as potências, depois as multiplicações e só por último as somas e subtrações.
E assim, chegamos no nosso resultado. Idêntico ao que vimos no gráfico.
Obs. O que fizemos no final das contas, foi só substituir o por na função que ele deu e encontrar o resultado dela. Aí você se pergunta: Então, por que demos essa volta ao mundo?
Bom, nem sempre o valor que a gente obtém quando faz essa substituição direta é uma valor válido. Por isso precisamos sempre começar tentado substituir pra conferir se dá certo. Caso a gente não consiga resolver dessa forma, procuramos outros meios de resolução. Mas sempre vamos começar tentando substituir, ok? 😊