Utilize as propriedades de limite para resolver a questão abaixo
Passo 1
FALA AÍÍÍ!! Para resolver essa questão precisamos utilizar as propriedades de limites, certo?! Então vamos lááá!!

Podemos começar aplicando a propriedade do limite da diferença! Afinal, temos dentro do limite a diferença entre dois termos, rs! Essa propriedade nos diz que o limite da diferença é igual a diferença dos limites! Ou seja,
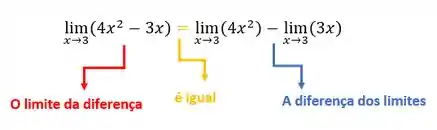
Beleza?!
Passo 2
Agora podemos aplicar a propriedade do limite do produto, pois se você reparar temos o multiplicando o e o multiplicando o . Tá... mas o que diz essa propriedade?

A propriedade do limite do produto diz que o limite do produto é igual ao produto dos limites. Vamos olhar primeiro para o
Assim,
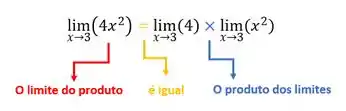
Show de bola?!
Passo 3
Vamos seguir o mesmo raciocínio para a outra parcela
Assim,
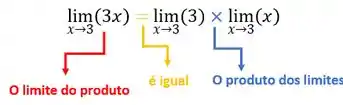
Beleza?!
Agora vamos juntar tudo! Vamos ficar com
Por fim, aplicaremos o limite em cada parcela
E assim temos a nossa resposta
Show de bola?!