Determine a soma dos limites indicados abaixo:
Passo 1
Oiee, olha nós aqui novamente! E vamos partir pra mais uma questão “filé” de limites.
Bom, a questão pede pra gente resolver essa soma de limites.
E a primeira coisa que temos que ter atenção é que cada limite tende pra um valor diferente. Então, não podemos misturar as coisa, ok?
Ahhh, mas tem esse esquisitos ali! Fica tranquilo que esse é o logaritmo, e ele não vai ser um problema pra gente. já já a gente fala sobre ele. Vamos primeiro ver o que podemos fazer para aplicar o limite em cada parcela. 😉
Passo 2
Há uma propriedade dos limites específica pra quando vamos calcular o limite de um logaritmo. Ela nos diz que podemos levar o limite pra dentro do logaritmo e aplicá-lo a função que estiver lá dentro, e depois calculamos o logaritmo do resultado. Assim, nosso limite que era:
Se torna:
Passo 3
Agora podemos aplicar o limite em cada caso. Para isso nós tiramos o operador do primeiro e substituímos o por , e tiramos também o operador do segundo e substituímos o por . Ficando com:
Beleza, o limite já foi, agora o que nos resta é resolver essa expressão aí. Faremos isso no próximo passo.
Passo 4
Para resolver a expressão, começamos com as continhas que estão dentro dos logaritmos.
Beleza. Agora é hora de calcularmos os ’s.
Mas o que é o logaritmo? Na verdade, o logaritmo é o valor do expoente que devemos colocar numa base (que é esse valor pequenininho que fica embaixo do )pra que
resulte no número que teremos dentro dos parênteses. Veja no esquema:
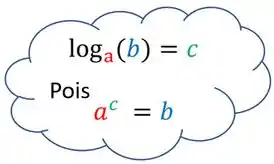
Logo, o que queremos saber é quem deve ocupar o lugar desse verdinho aí.
Ou seja:
O está perguntando pra gente, qual é o valor que devemos elevar o para encontrar como resultado o . E a resposta é , porque .
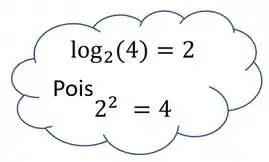
E o está perguntando pra gente, qual é o valor que devemos elevar o para encontrar como resultado o . E a resposta é , porque .
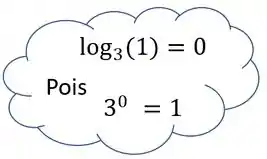
Com isso, temos:
Viu como entendendo o que a questão queria direitinho a gente conseguiu resolver?
E esse é o nosso resultado! 😁