A velocidade de lançamento de um projétil é cinco vezes maior que a velocidade na altura máxima. Determine o ângulo de lançamento
Passo 1
Vamos para mais uma, galerinha?!
Vamos começar desenhando o que está acontecendo
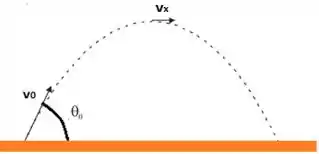
É importante vocês lembrarem que na altura máxima não há velocidade na direção porque atingimos o ponto mais alto e agora é a hora dele descer!! Sendo assim, a velocidade neste ponto é igual a velocidade na direção
Na direção não há aceleração, então o movimento é uniforme e é a mesma ao longo de toda a trajetória!
Bom, o problema nos disse que a velocidade de lançamento de um projétil é cinco vezes maior que a velocidade na altura máxima:
Vamos guardar esta infomação no coração, ok?
Passo 2
Vamos dar uma olhada mais de perto na relação entre e
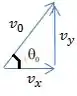
Segundo a trigonometria:
Neste caso:
Como já vimos no Passo que , então
Simplificando o em cima e em baixo
Agora para encontrar o ângulo , precisamos pensar num ângulo cujo arco seja igual a . Então o será o arco cosseno de
Como não somos uma máquina, precisamos recorrer a calculadora para encontrar esse ângulo. Mas na sua calculadora a opção de pode estar escrita assim
Que é a mesma coisa. O resultado será
O que acharam desta?!