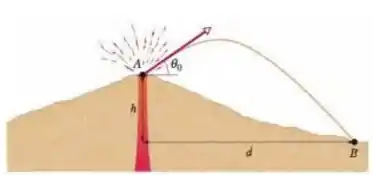
Durante as erupções vulcânicas, grandes pedaços de pedras podem ser lançados para fora do vulcão, são os projéteis que estão na mesma altitude do monte fuji.a) Com que velocidade inicial um bloco vulcânico deve ser ejetado com ângulo de em
relação a horizontal a uma distância .
b) Qual o tempo de voo?
Dados: Altitude o monte fuji
Passo 1
Bora seguir?! Vamos começar desenhando nossos eixos de referência
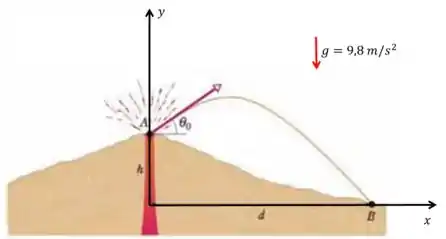
Sabemos que o projétil percorreu na direção horizontal, certo? Então podemos dizer que a posição inicial dele no eixo é
e a posição final será
Passando para metros
Também sabemos que na direção do movimento não há aceleração, já que a gravidade aónta para baixo e não para a esquerda ou para a direita. Então o movimento é uniforme!!
Nesse caso vamos usar
Substituindo esses valores na fórmula, ficamos com
ou seja,
Mas não temos nem o !
Mas sabemos que existe uma relação entre , e
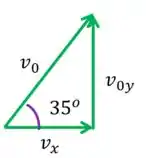
Segundo a trigonometria
Nesse caso
Para achar , vamos passar o multiplicando para o outro lado
Substituindo na fórmula que encontramos alí em cima
Passando o e o para o outro lado dividindo
Então, para achar a velocidade inicial, que foi pedida na letra (a), precisamos do tempo, que foi pedido na letra (b)! Então faremos o inverso, acharemos (b) e depois (a)!!
Mas anotem essa formulinha aí para não esquecer, vamos voltar nela já já.
Passo 2
O tempo para o projétil cair, ou seja, o tempo que ele fica no ar, será o tempo que ela leva para subir mais o tempo que ela leva para descer:
Como o projétil leva o mesmo tempo para descer e para subir:
Então:
Então só precisamos do tempo de subida!!
Quando o corpo se move na direção vertical, existe aceleração (a da gravidade)!! E nestes casos o movimento é MRUV!!
No ponto mais alto, vimos que não há velocidade na direção , somente na
Sabendo de tudo isso podemos usar a equação:
A altura do monte Fuji será a posição inicial da pedra no eixo e essa altura foi um dado do enunciado
Passando para metros
Show! Outra coisa que podemos concluir é que a posição final da pedra será quando ela atingir o chão, o ponto mais baixo da trajetória. Então
A única coisa que não temos é !! Mas olhando a relação do Passo :
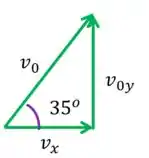
Segundo a trigonometria:
Neste caso:
Para achar , vamos passar o multiplicando para o outro lado:
Além disso, também sabemos que a aceleração da gravidade aponta sempre para baixo e nosso eixo aponta para cima. Olhem o desenho novamente
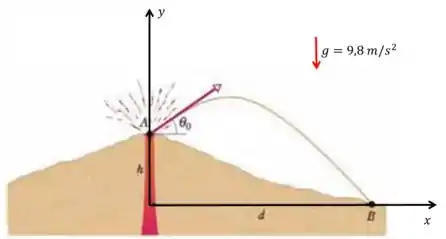
Então colocaremos um sinal de menos na aceleração, belezinha?
Colocando todos os dados na fórmula:
O Passo 1 nos deu uma expressão para , lembram dela? Pedi para anotar para não esquecer hehe
então vamos substituir isso também
E lembrando que
O no segundo termo pode cancelar, já que estão presentes no numerador e denominador:
Então:
Vamos resolver primeiro aquela meiuca alí
Agora faremos a soma
O termo passa para o outro lado com sinal oposto:
E agora o passa dividindo:
Tiramos raiz dos dois lados:
Encontramos o tempo de subida como aproximadamente
Então o tempo total será
Fazendo essa multiplicação encontraremos o tempo total
Show! Encontramos a resposta para a letra (b), mas deixamos a letra (a) pendente, lembra?
Passo 3
Agora podemos achar a letra (a) !! Bora substituir este tempo na equação do Passo ?
Bem legal, não foi ?!