Um projétil de massa é lançado obliquamente a partir do solo, para o alto, numa direção que forma com a horizontal com velocidade de , primeiro na Terra e posteriormente na Lua. Considerando a aceleração da gravidade da Terra o sêxtuplo da gravidade lunar, e desprezíveis todos os atritos nos dois experimentos, analise as proposições a seguir:
- A altura máxima atingida pelo projétil é maior na Lua que na Terra.
- A velocidade do projétil, no ponto culminante da trajetória será a mesma na Lua e na Terra.
- O alcance horizontal máximo será maior na Lua.
Passo 1
Vamos começar uma teórica, para quebrar um pouco as continhas.
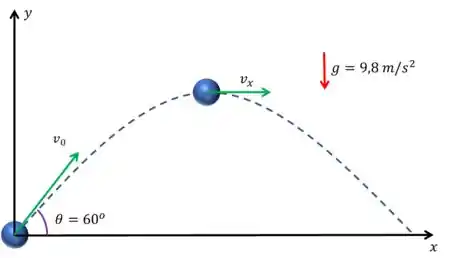
Como no tópico ele quer comparar a altura máxima na Lua e na Terra, precisamos lembrar que quando o projétil está se movendo na direção vertical, existe aceleração (a da gravidade)!! E nestes casos o movimento é MRUV e podemos usar essas equações aqui
Para saber qual delas utilizar, precisamos olhar as informações que temos.
No ponto mais alto vimos que não há velocidade na direção , somente na Então
Sabemos também que a aceleração da gravidade aponta sempre para baixo e o nosso eixo está para cima. Então teremos uma aceleração negativa!
Nesse caso não substituiremos o valor da gravidade da terra porque não foi dado no enunciado e essa é uma questão teórica.
E temos mais duas informações com relação as posições. A primeira é que a posição inicial em é zero
E a posição final é a altura máxima, que chamaremos de
Agora é a hora de escolher a equação baseado nessas informações!
Passo 2
Como não sabemos nada sobre o tempo e nem estamos interessados em calculá-lo, a única equação que não envolve o tempo é a terceira, a equação de Torricelli
Substituindo só o que temos:
Lembrando da regrinha da multiplicação que “sinais iguais é sempre mais e sinais diferentes é sempre menos”, como temos uma multiplicação de um número positivo por um negativo, então
Para isolar a altura máxima, o termo passa para o outro lado com sinal oposto
E o passa dividindo
Bom, é o mesmo tanto para o lançamento na Terra quanto na Lua, não é? Então não nos preocuparemos com ele.
Vamos olhar apenas para a gravidade, pois a da Terra é diferente da da Lua e o enunciado deu essa relação para nós. Ele disse o seguinte
Escrevendo isso em matematiquês, teremos
Achando a altura máxima para os dois casos:
Substituindo pelo que o problema nos disse:
Vamos colocar este separado para facilitar nossa análise
O termo nós sabemos que é , então é só substituir
Passando o multiplicando
Então, a altura máxima na Lua é seis vezes maior que a altura máxima na Terra!!
Concluindo que a afirmativa está correta!!
Passo 3
A afirmativa nos diz que a velocidade do projétil, no ponto culminante da trajetória será a mesma na Lua e na Terra!
É importante vocês lembrarem que “ponto culminante” significa a parte mais alta da trajetória, ok?
O que vocês acham?
Neste ponto não há velocidade na direção porque atingimos o ponto mais alto e agora é a hora dele descer!! Sendo assim, a velocidade neste ponto é igual a velocidade na direção
Vamos dar uma olhada mais de perto na relação entre , e :
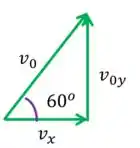
Segundo a trigonometria:
Neste caso:
Para achar , vamos passar o multiplicando para o outro lado:
Como a velocidade inicial tanto na Lua quanto na Terra é a mesma e o ângulo também, então esse resultado será o mesmo nos dois lugares!
Por incrível que pareça, a velocidade no ponto mais alto das duas trajetórias será a mesma
E a afirmativa II é verdadeira!!
Passo 4
Na afirmativa diz que o alcance horizontal máximo será maior na Lua, certo?
O alcance é o quanto o projétil percorre na direção , como nessa direção não há aceleração, o movimento é uniforme!!
E qual fórmula usamos neste caso?
Já sabemos que
Porque parte da origem. Então nossa equação se reduz a
Já vimos que a velocidade no eixo não varia, então poderíamos falar que o alcance não vai mudar! Mas temos um porém!!
O tempo que o objeto permanece no ar depende do seu movimento na direção concordam?
O projétil leva um tempo para subir em um tempo para descer, então o tempo total será
Como o movimento de subida e descida são iguais, podemos escrever
Colocando na fórmula:
E como calculamos este tempo de subida? Como existe acleleração o movimento é uniformemente variado, e podemos optar pela fórmula:
Como já sabemos que a aceleração tem que ser negativa porque a gravidade aponta para baixo e o eixo aponta para cima
E no ponto máximo já vimos que
Podemos substituir isso na fórmula
Passando o termo para o outro lado com sinal oposto
E a gravidade passa dividindo
Aplicando isso na fórmula do alcance que descobrimos alí em cima
Ficaremos com
Agora vamos substituir as gravidades?
Como
Substituindo
Vamos colocar este separado para facilitar nossa análise:
O termo nós conhecemos, então é só substituir:
Passando o multiplicando:
Então, realmente, o alcance é maior na Lua!!
E a afirmativa é verdadeira!!
Bora seguir?
Resposta
I – Correta;
II - Correta;
III – Correta.