Um projétil lançado para cima, sob um ângulo de ° com a horizontal, tem velocidade de no ponto culminante de sua trajetória. Calcule a velocidade do projétil ao retornar ao solo.
Passo 1
Falaaa aiiii galeraaaa, animados para começar esta seção?
Espero que siiim ein!!
Vamos começar desenhando o que está acontecendo:
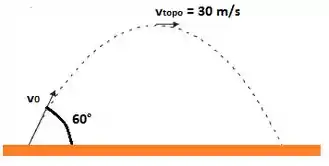
É importante vocês lembrarem que ponto culminante significa a parte mais alta da trajetória, ok?
Neste ponto não há velocidade na direção porque atingimos o ponto mais alto e agora é a hora dele descer!! Sendo assim, a velocidade neste ponto é igual a velocidade na direção
Na direção não há aceleração, então o movimento é uniforme e é a mesma ao longo de toda a trajetória!
Vamos guardar esta infomação no coração, ok?
Passo 2
Bom, mas o que queremos é a velocidade final!! Ou seja, a velocidade do projétil quando ele toca no chão!!
Para resolvermos esta questão precisamos lembrar que a velocidade com que ele chega é igual a velocidade com que ele sai:
Então só precisamos achar !!
Vamos dar uma olhada mais de perto na relação entre e
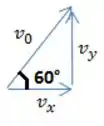
Segundo a trigonometria:
Neste caso:
Para achar , vamos passá-lo multiplicando para o outro lado:
E agora o cosseno passa para o outro lado dividindo:
E agora é só substituir
Na fórmula que encontramos do
Então:
Legal, não foi?!