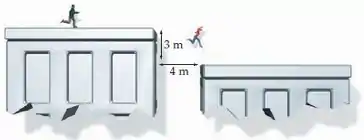
Um policial persegue um mestre ladrão de joias pelos telhados da cidade. Ambos estão correndo quando chegam a um vão entre edifícios de de largura e uma queda de (Figura 3-19). O ladrão, tendo estudado um pouco de física, salta a , em um ângulo de acima da horizontal, e salta a lacuna facilmente. O policial não estudou física e acha que deveria maximizar sua velocidade horizontal, então ele salta horizontalmente a . (a) Ele consegue chegar do outro lado? (b) Por quanto o ladrão consegue chegar ao outro lado?
Passo 1
Bora pra mais uma?!
Bom galerinha, precisamos descobrir se o policial consegue ou não chegar na outra coluna, certo?
Ou seja, precisamos saber se ele consegue ou não percorrer uma distância de na direção horizontal! Sabemos que na direção não há aceleração e o movimento é uniforme, nestes casos a única possibilidade que temos é usar a relação para a velocidade:
Para saber a posição inicial e final do policial precisamos definir os eixos. Vamos dar um zoom no momento do salto do policial
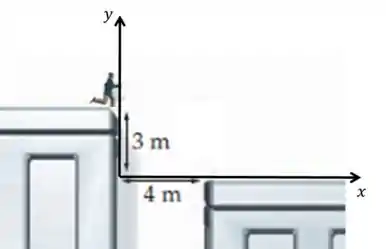
Beleza, agora foquem apenas no eixo . Repare que o policial comoça no início (cê jura? kkk). Então
E o enunciado nos diz a velocidade no eixo do policial
Substituindo esses dados na fórmula, ficamos com
Nas não foi dado o tempo ☹
Passo 2
Então vamos usar o deslocamento dele na vertical para encontrar o tempo que o policial leva para cair , ok?
O policial começa seu movimento quando
E queremos saber o tempo que ele leva para cair até
Como a velocidade inicial dele é toda na horizontal, então sua velocidade inicial na vertical será
E temos também a influência da gravidade que sempre aponta para baixo. Como definimos o eixo para cima, então nossa aceleração será negativa, beleza?
Com todas essas informações em mente, precisamos olhar para as equações do MRUV
E descobrir qual delas utilizar.
Passo 3
Como precisamos do tempo, então já eliminaremos a terceira equação.
Não estamos interessados na velocidade final e nem sabemos quanto ela vale, então eliminamos a segunda.
Sobrou apenas a primeira, vamos usar ela então 😊
Substituindo o que já temos:
Passando o para o outro lado com o sinal contrário
O termo passa dividindo:
Aplicando a raiz de ambos os lados:
E com o tempo podemos achar a distância colocando ele lá na fórmula que vimos no Passo
E o policial caiu no buraco, por pouco, mas caiu!!
Passo 4
Na letra (b) queremos saber por qual distância o ladrão consegue se safar e não cair no buraco, certo?
Para saber disso, precisamos saber o deslocamento dele na direção , e novamente podemos usar a relação obtida no Passo
Não temos nem o do ladrão nem o tempo do salto!
Vamos dar uma olhada mais de perto na relação entre , e
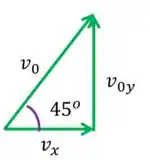
Segundo a trigonometria
Neste caso
Para achar e , vamos passar multiplicando para o outro lado
Sabemos que
Então só vamos precisar de substituir
De boa, não foi?!
Passo 5
Achamos as componentes da velocidade, mas nada do tempo, certo?
Utilizaremos a mesma equação do Passo para o policial, mas agora para o ladrão
E agora colocando nossos dados para o ladrão
Não esqueceram que a gravidade aponta para baixo, por isso nossa aceleração fica negativa, né?
Vamos substituir na equação
Passando todo mundo para o lado esquerdo da equação, ficaremos com
Para resolver uma equação de segundo grau usamos a fórmula quadrática (o famoso Baskara)
Quem acompanha o é chamado de o que acompanha o chama-se e o solitário é o Então, olhando a equação:
Colocando na fórmula quadrática:
Teremos dois valores para , um quando o sinal alí do meio for positivo e outro quando for negativo
Como o tempo dever ser positivo (a menos que tenhamos um viajante do tempo haha)
E agora que achamos tudo, usamos estes valores para achar
Portanto, o ladrão percorreu na direção , como a lacuna tinha uma distância de o ladrão aterrissou a da beirada!!
Legal, não foi?!