Na Fig. uma pedra é lançada em um rochedo de altura com uma velocidade inicial de e um ângulo com a horizontal. A pedra cai em um ponto , após o lançamento. Determine
(a) a alutura h do rochedo,
(b) a velocidade da pedra imediatamente antes do impacto em e
(c) a máxima altura alcançada acima do solo.
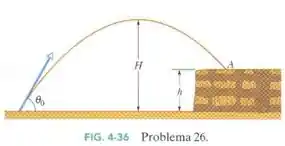
Passo 1
Vamos continuado galerinha??
Bom, como a velocidade inivia da pedra faz ela se mover tanto de baixo para cima (eixo ) quanto da esquerda para direita (eixo ), precisamos separar esse movimento nesses dois eixos. Então vamos definir esses eixos e colocar as informações que foram dadas no enunciado
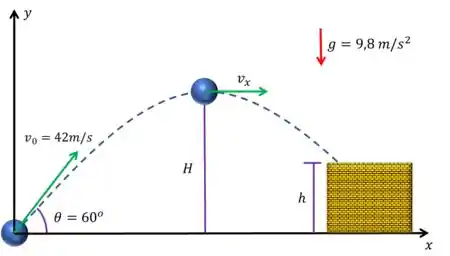
Como a letra (a) pediu a altura do rochedo precisamos avaliar este movimento na direção , já que essa altua se mede na vertical.
Como temos uma aceleração da gravidade apontando para baixo (eixo ), então o movimento no eixo será uniformemente variado e teremos que usar essas equações aqui
Agora a pergunta que não quer calar: Qual dessas equações que temos que usar? Bom... para responder a essa pergunta precisamos olhar as informações do enunciado e ver o que está querendo que seja calculado, vamos lá!
Como a pedra parte da posição mais baixa da trajetória, vamos dizer que ela sai da posição
Essa pedra parte com uma velocidade inicial
Mas essa velocidade inicial está inclinada formando um ângulo de
Então temos que descobrir qual a velocidade inicial no eixo , já que e nele que estamos trabalhando. Para isso, basta lembrar da relação entre e .
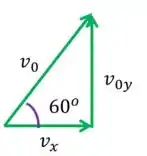
A trigonometria diz que:
Neste caso:
Para achar , vamos passar o multiplicando para o outro lado:
Como já sabemos que e o podemos colocar na calculadora, então
E ainda temos mais uma informação importante, a da aceleração. Nesse caso nossa aceleração será a da gravidade! Mas como a gravidade aponta sempre para baixo e nosso eixo aponta para cima, então vamos colocar um sinal de negativo, beleza?
E também foi dado o tempo que a pedra leva para chegar até em cima do muro
Maravilha! Essas são todas as informações do eixo , agora temos que escolher uma daquelas equações, vem comigo!
Passo 2
Vamos colocar as informações todas juntas aqui pra ficar melhor de visualizar
Agora qual dessas equações utilizar?
Vou te dar umas dicas. Bem... já sabemos o tempo, então podemos eliminar a terceira equação. Não sabemos a velocidade final da pedra, então a segunda também não será interessante. Restou apenas a primeira e já temos todas as informações dela!
Vamos fazer essa conta juntos
E isso dá pra gente
Uhuuuulll! Resolvemos a letra (a)
Passo 3
Agora vamos tentar achar a velocidade final da pedra?
O movimento ocorre em duas dimensões, e então a velocidade final deve ter duas componentes!!
Como o na direção não possui aceleração, a velocidade inicial nesta direção é a mesma ao longo de toda a trajetória!!
Usando o triângulo do Passo
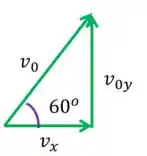
e com ajuda da trigonometria:
Neste caso:
Para achar , vamos passar multiplicando para o outro lado:
Substituindo:
Show! Já encontramos a velocidade final no eixo . Agora vamos encontrar no eixo .
Se estamos no eixo novamente, então temos que usar uma daquelas equações
Como agora estamos interessados na velocidade final, vamos utilizar a segunda equação substituindo essas informações aqui que já sabemos
Vamos substituir
Pela ordem das operações, temos que resolver a multiplicação primeiro, então
Como o número maior é o negativo, então nossa resposta será negativa
Ooxe, que coisa estranha, Por que será que ficou negativo? Lembra que definimos o eixo para cima e tudo o que estiver apontando para baixo será negativo? Então, isso mostra que a velocidade final em é para baixo, o que super faz sentido já que a pedra está descendo, não é?
Show! Já temos as velocidades no eixo e no eixo . Agora temos que combinar as duas para encontrar a velocidade final total. Vamos olhar como ficam as velocidades quando a pedra chega em cima do muro
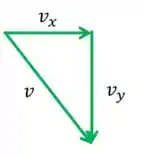
Como já sabemos que
Então podemos usar o teorema de Pitágoras para encontrar . Lembra como funciona?
Tirando a raiz quadrada dos dois lados, temos
Subsituindo:
Passo 4
E para finaliza, a letra (c) quer a altura máxima!!
E para lançamentos oblíquos existe uma fórmula bem legal e beem prática:
Essa fórmula já nos fornece a altura máxima e nos poupa de muito trabalho (mais do que já tivemos até aqui kkk).
Substituindo os dados:
Molezinha, não foi?