Um corpo é lançado para cima segundo um ângulo de com a horizontal, com velocidade de . Admitindo-se pedem-se:
- O tempo que o corpo leva para atingir a altura máxima em relação ao solo;
- A altura máxima;
- O alcance.
Passo 1
Vamos para mais uma, galerinha ?!
Vamos começar desenhando o que está acontecendo:
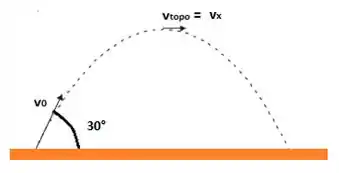
É importante vocês lembrarem que na altura máxima não há velocidade na direção porque atingimos o ponto mais alto e agora é a hora dele descer!! Sendo assim, a velocidade neste ponto é igual a velocidade na direção
Na letra (a) o que queremos é achar o tempo que o corpo leva para atingir o ponto mais alto, certo? Vamos chamar esse tempo de , que é o tempo de subida
Quando o corpo se move na direção vertical, existe aceleração (a da gravidade)!! Como a gravidade aponta para baixo e definiremos o eixo para cima, então nossa aceleração será negativa, beleza?
No ponto mais alto, vimos que não há velocidade na direção , somente na Então
Sabendo de tudo isso podemos usar a equação:
Que substituindo as informações que escrevemos aí em cima
O termo passa para o outro lado com sinal positivo
E agora o vai dividindo
Ainda não temos a velocidade inicial na direção , mas olhando mais de perto a relação entre , e
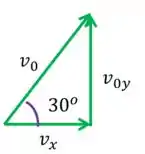
Segundo a trigonometria:
Neste caso:
Para achar , vamos passar o multiplicando para o outro lado:
Sabendo o valor de e do
Substituindo na fórmula do tempo:
Encontramos que o tempo de subida é, aproximadamente
Tranquilinho?!
Passo 2
Na letra (b) queremos a altura máxima, não é?
Podemos escolher qualquer uma das outras equações do MRUV, ok? Vou optar por:
Já sabemos que no ponto mais alto:
E também temos na parte inicial
Substituindo:
E vamos para a últimaa!!
Passo 3
Agora vamos tentar achar a que distância do seu ponto de lançamento o projétil aterrissa!!
O tempo para o projétil cair será o tempo que ela leva para subir mais o tempo que ela leva para descer
Como o projétil leva o mesmo tempo para subir e para descer
Então
Como , podemos substituir
Bom, agora que sabemos disso precisamos lembrar que na direção do movimento não há aceleração, ou seja o movimento é uniforme!!
Nestes casos vamos usar
Como a posição inicial no eixo é zero
Nossa fórmula se reduz a
Mas não temos , certo? Então, olhando novamente a relação entre , e :
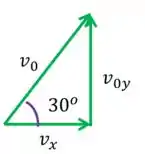
Segundo o trigonometria:
Neste caso:
Para achar , vamos passar o multiplicando para o outro lado:
Substituindo a velocidade inicial nesta fórmula:
Substituindo na fórmula do alcance:
O que acharam desta ?!