Uma graduada em física joga uma bola pelo o ar com uma velocidade inicial de a acima da horizontal. A bola é posteriormente capturada por outro aluno. Encontre (a) o tempo total em que a bola fica no ar e (b) a distância horizontal total percorrida. (Ignore os efeitos da resistência do ar).
Passo 1
Animados para seguir?!
Então bora desenhar!!
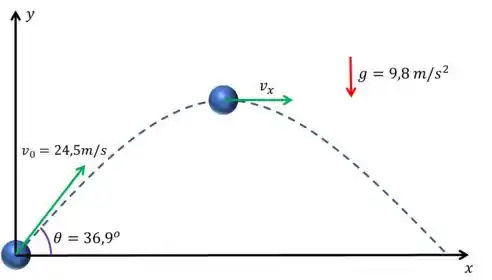
Para resolver este problema aqui precisamos assumir que a bola sai da altura zero e o outro aluno a pega na mesma altura, tranquilinho?
Para calcular o tempo que a bola fica no ar vamos usar as relações para o movimento na direção , porque na direção praticamente não há dados!
Show! Já entendemos o que está acontecendo, já sabemos qual fórmula utilizar, agora precisamos anotar as informações que temos até agora.
Passo 2
Olhando apenas para o eixo nós sabemos que a posição inicial tem que ser
e a posição final é quando a bola toca o solo novamente, então a posição final em também tem que ser zero
Além disso, como estamos assumindo que o eixo aponta para cima, esse será nosso eixo de referência. Então a gravidade, por apontar para baixo, será negativa
Agora precisamos descobrir quem é a velocidade inicial em para aplicar na nossa fórmula. Vamos lá!
Não sabemos a velocidade inicial em , mas sabemos que existe uma relação entre as velocidades. Observem o desenho
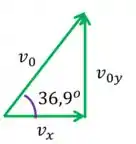
Segundo a trigonometria:
Neste caso:
Para achar , vamos passar o multiplicando para o outro lado:
Como já sabemos que e o podemos colocar na calculadora, temos
Fazendo essa continha encontraremos o
Maravilha! Agora só temos que substituir na fórmula.
Passo 3
Recaptulando tudo o que já temos
E nossa fórmula era
Substituindo geral, teremos
Passando o para o outro lado, ele vai positivo
Repare que se colocarmos a equação estará correta, pois dará . O que isso significa? Significa que no instante a bolinha estava passando pelo ponto em que , o que está correto!
Mas nosso interesse é no outro ponto, então vamos simplificar por dos dois lados
ficaremos com
Agora podemos passar o para o outro lado dividindo
E assim chegamos ao fim da letra (a) !!
Passo 4
Precisamos achar a distância horizontal total percorrida, ou seja, o alcance!!
Na direção não há aceleração, então usamos a fórmula para o movimento uniforme:
Como a posição inicial no eixo é zero,
Nossa fórmula se resume a
Lembrando do triângulo do Passo
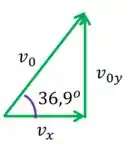
Segundo a trigonometria:
Neste caso:
Para achar , vamos passar o multiplicando para o outro lado:
Como já sabemos que e o podemos colocar na calculadora, temos
Fazendo essa continha encontraremos o
Show! Agora precisamos substituir todo mundo na fórmula.
Passo 5
Relembrando as informações úteis até agora
Vamos substituir na fórmula
E assim finalizamos mais uma!!