Quando um balão científico desgarrado está subindo a , um dos instrumentos se desprende e cai em queda livre. A figura mostra a velocidade vertical do instrumento em função do tempo, desde alguns instantes antes de se desprender até o momento em que atinge o solo.
- Qual é a altura máxima que o instrumento atinge em relação ao ponto em que se desprendeu?
- A que altura acima do solo o instrumento se desprendeu?
Passo 1
Bora pra mais uma?!
Bom galerinha, vamos começar essa questão entendendo o que esse gráfico está nos dizendo.
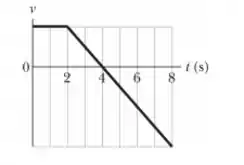
Como ele começa com uma linha horizontal até o tempo de , significa que a velocidade permaneceu constante, ou seja, o instrumento ainda está preso no balão.
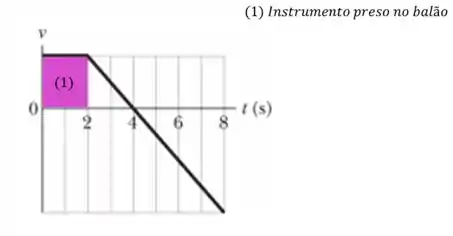
A partir de , a velocidade começa a diminuir. Isso indica que o objeto se desprendeu do balão exatamente nesse ponto, mas sua velocidade continua positiva, então o objeto ainda está subindo, mas perdendo velocidade.
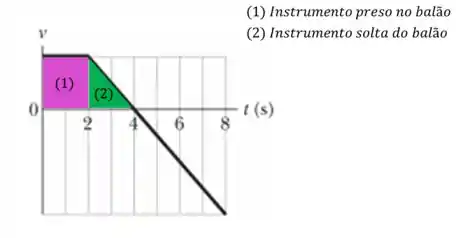
Quando a velocidade é zero, significa que o instrumento chegou na altura máxima!
Opa! Chegamos no ponto que queremos para a letra (a)! Então vamos utilizar o tempo a partir do ponto que o instrumento se desprende do balão, , até o ponto de altura máxima, em .
Ou seja, o intervalo de tempo que usaremos é
Agora vou dar uma dica de ouro para vocês. Quando tivermos um gráfico de velocidade pelo tempo, a área do gráfico será o valor exato do deslocamento do objeto, que no nosso caso será a altura!
Como a figura formada é um triângulo na parte , a área é dada por:
A altura é dada ela velocidade:
E a base é o intervalo de tempo:
Substituindo:
E assim terminamos a letra (a) !!
Passo 2
Na letra (b) precisamos achar altura acima do solo que o instrumento se desprendeu, certo?
Como o instrumento leva o mesmo tempo para subir e para descer, se o instrumento leva para chegar a sua altura máxima ( até ) os próximos ele vai descer da altura máxima até o ponto em que o instrumento se desprendeu ( até )!!
Então, o instrumento chega ao solo no intervalo de 6 até 8!!
Se o balão está subindo, existe a aceleração da gravidade, e o movimento é retilíneo uniformemente variado. Neste caso poderemos usar a relação:
Assumindo que a altura em que o instrumento se desprendeu é o ponto inicial e a velocidade também:
Como o instrumento desceu por
Vamos substituir?
Legal, não foi?!