Calcule o tempo gasto para um objeto cair de uma altura de , supondo que ele parte do repouso e não sofre resistência do ar durante a queda.

Bora pra mais uma ?!

Vamos começar desenhando o que está acontecendo:

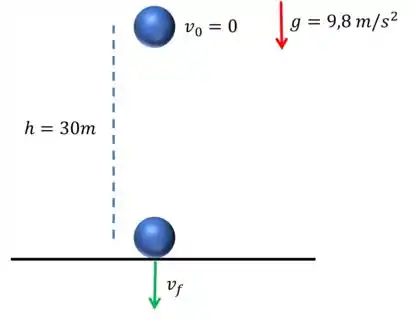
Já sabemos que quando um objeto está caindo existe uma aceleração aplicada neste corpo, certo? A aceleração da gravidade !!

Sendo assim podemos usar as equações para o MRUV, certo?

Mas qual fórmula usar?

Vamos ver as informações que temos do enunciado, mas antes precisamos definir nosso eixo de referência para usar os sinais de forma correta.

Vamos definir que tudo o que apontar para cima será positivo e tudo o que apontar para baixo será negativo, beleza? Então nosso eixo fica assim

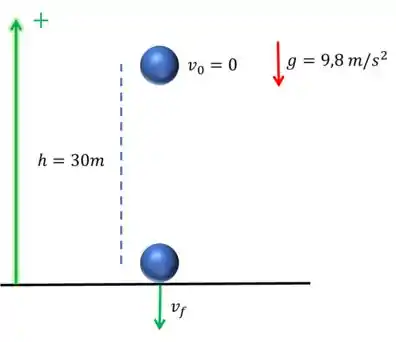
Como , isso significa que a posição inicial do objeto é

E como o objeto cai no chão, então a posição final dele será

Perceba que a gravidade, por apontar para baixo, receberá um sinal de negativo para ficar coerente com o nosso referencial. Então

E também sabemos que o objeto parte do repouso, então

Show! Agora vamos olhar as equações do MRUV

E comparar com os dados que temos

Como precisamos do tempo, então poderíamos escolher a ou a . Mas não temos , então descartaremos a e utilizaremos a equação

Substituindo os valores

Passando o para o outro lado da equação, ficará positivo

O termo passa dividindo para o outro lado:

Aplicando a raiz dos dois lados para remover este “ao quadrado”:

E finalizamos mais umaa !!