Um balão de ar quente está subindo a uma taxa de e está a acima do solo quando um tripulante deixa cair um pacote.
- Quanto tempo o pacote leva para atingir o solo?
- Com que velocidade atinge o solo?
Passo 1
Vamos seguindo?!
Vamos ver o que está acontecendo?
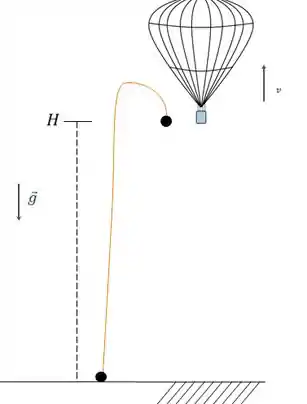
Bom galerinha, o objeto se desprende em um certo ponto, ok? O balão estava subindo com uma certa velocidade, então quando ele se desprende, por inércia, o instrumento sobe mais um pouco antes de cair até que a velocidade se anule!!
Quando o objeto atinge sua altura máxima e começa a descer, tranquilo?!
Vamos ver quanto tempo o objeto leva até alcaçar Para isso vamos usar uma das equações do MRUV:
Lembrando que:
Oxe, por que a aceleração ficou negativa?? Ficou negativa porque estamos assumindo um referencial positivo para cima! Então tudo o que estiver para cima será positivo e tudo o que for para baixo será negativo, belezinha?
Substituindo:
O termo passa para o outro lado com sinal oposto:
E agora passa para o outro lado dividindo:
Durante este tempo, o objeto sobe mais um pouquinho, certo? Vamos ver a distância em que ele se encontra do chão usando:
Substituindo os valores que já temos:
Não esqueceu que a gravidade fica negativa porque ela aponta para baixo, né!?
Fazendo essa continha ficamos com
Beleza !!
Passo 2
Quando o objeto atinge esta altura, ele começa a descer, para achar o tempo de descida podemos usar a mesma relação que a anterior:
Analisando só a descida:
Então:
O termo passa para o outro lado da igualdade com sinal oposto:
Agora o passa dividindo:
Aplicando a raiz dos dois lados:
E o tempo total é a soma do que ele leva para subir e descer:
Bora pra (b)?!
Passo 3
Agora precisamos saber a que velocidade o objeto atinge o solo, certo?
Como já sabemos o tempo de descida e a velocidade inicial a partir da altura máxima
Podemos usar a fórmula:
Podemos escolher outras, mas optei por esta pois achei que seria a mais tranquila neste caso!!
Sem equecer que a aceleração que usaremos é a da gravidade e esta aponta para baixo, então
Substituindo:
Vish, a velocidade final ficou negativa, será que erramos em algum lugar? Não, pequeno gafanhoto, lembra que quando uma grandeza é negativa significa que está apontando para baixo (já que definimos que o positivo é para cima)? Então... Isso mostra que a velocidade do objeto quando chega ao solo está apontando para baixo, o que é súper coerente 😊
Legal, não foi?