Da beira de um barranco situado a em relação ao nível inferior do solo, um garoto chuta uma bola imprimindo-lhe uma velocidade horizontal de . Na parte inferior do barranco, da vertical do primeiro garoto, um outro garoto vai tentar pegar a bola. Determine a que distância, à frente ou atrás, do segundo garoto, a bola chutada cairá.
Passo 1
Bora pra mais uma ?!
Vamos começar desenhando o que está acontecendo:
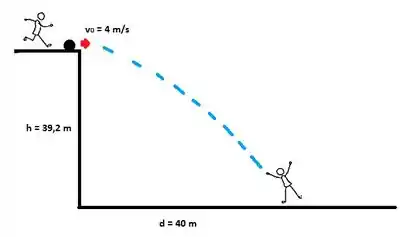
É importante percebermos aqui que nós queremos saber a que distância do barranco a bola cai!!
Esta distância está relacionada a quanto a bola percorre na direção do eixo , neste sentido não há nenhuma aceleração sendo aplicada na bola, e seu movimento é uniforme!! Quem aí se lembra da fómula para este movimento?
A velocidade na direção já foi dada, mas não temos o tempo nem a distância!
Então precisamos descobrir este tempo, para poder calcular qual a distância a bola percorreu, tranquilo?
O tempo para a bola percorrer esta distância é o mesmo para a bola chegar ao solo, ou seja, percorrer a altura
Só que na direção vertical existe aceleração da gravidade e, por isso, o movimento é uniformemente variado !!
Nestes casos existem duas fómulas que podemos usar que possuem a variável de interesse, o tempo:
Agora precisamos prestar atenção nas informações que podemos substituir e nos sinais!! Vamos começar com as informações. A bola começa lá de cima na altura e cai até chegar na altura
A velocidade inicial no eixo tem que ser zero, porque o menino chuta a bola na horizontal, então na vertical a velocidade é zero
Então substituindo essas informações na fórmula, ficaremos com uma expressão mais reduzida
Agora muito cuidado com os sinais! Vamos considerar que tudo o que estiver para cima será positivo e o que estiver para baixo será negativo. Como a aceleração é a da gravidade e ela aponta sempre para baixo, teremos
Então ficamos com
Sabendo que:
Substituindo:
Podemos passar o termo que tem para o outro lado com sinal contrário
Podemos simplificar o com o
O termo passa dividindo para o outro lado:
Aplicando a raiz dos dois lados para remover este ao quadrado:
Passo 2
Era isso que queríamos??
Que nada né !!
Queremos a distância , então vamos substituir na primeira equação que vimos:
Sabemos que:
Substituindo:
Como o garoto de baixo está a uma distância de , então a bola cairá bem antes do garoto de baixo!!