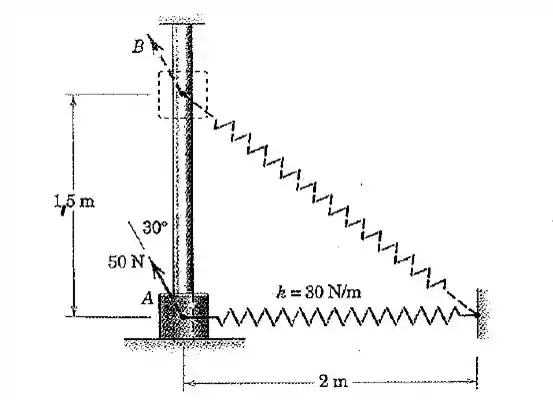
O cursor tem uma massa de e está preso à mola leve, que tem uma rigidez de e um comprimento sem deformação de . O cursor é liberado a partir do repouso em e desliza para cima na barra lisa sob a ação da força constante de . Calcule a velocidade do cursor quando este passa a posição .
Passo 1
Podemos usar:
No caso desse problema, existe sim uma força externa que realiza trabalho. Esse trabalho é dado por:
Passo 2
A variação de energia cinética será dada por:
E a variação de energia potencial gravitacional? Assim:
Passo 3
A variação da energia elástica será:
Quanto vale ? é o alongamento da mola no final. Pra isso, precisamos calcular o comprimento da hipotenusa daquele triângulo do enunciado e depois subtrair disso o valor do comprimento da mola não esticada:
E ? Segue o mesmo princípio, só que para o ponto inicial:
Assim:
Passo 4
Assim: