Um cursor com uma massa de é liberado a partir do repouso em e desliza para baixo e em torno do arame liso fixo. Determine a força entre o arame e o cursor quando este passa o ponto .
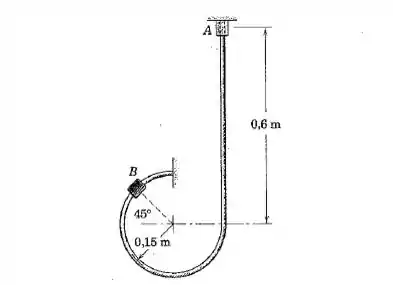
Passo 1
O sistema pode ser presentado por:
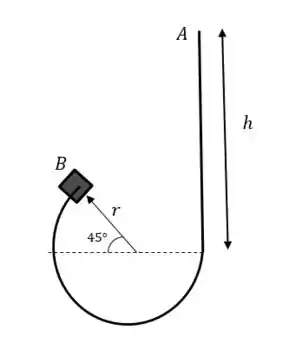
Vamos usar a seguinte fórmula:
No caso desse problema:
Assim:
Passo 2
Colocando a altura nula no centro do círculo, podemos dizer a variação da energia potencial gravitacional é dada por:
Passo 3
A variação da energia cinética é dada por:
Assim:
Vamos usar isso no próximo passo (:
Passo 4
As forças atuando na caixa serão:
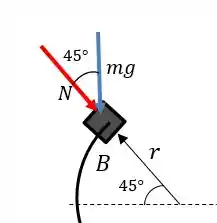
Como o corpo está rotacionando, teremos uma resultante centrípeta. Podemos escrever:
Assim, substituindo o :
Passo 5
Usando