Um satélite artificial que se desoloca em uma órbita elíptica tem uma velocidade de a uma altitude de km no ponto . Determine sua velocidade no ponto onde a altitude é . Considere a Terra como uma esfera de raio e use para a aceleração da gravidade na superfície da Terra.
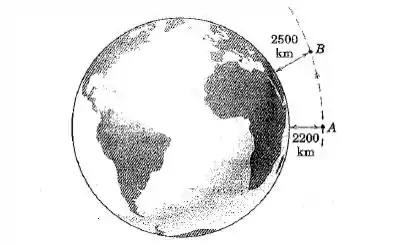
Passo 1
Aqui vamos usar a fórmula generalizada para a energia potencial gravitacional:
Onde é a distância até o centro da terra o próprio raio da terra.
Passo 2
Assim, a variação é dada por:
Assim:
Deixamos em função de porque não a conhecemos.
Passo 3
A variação de energia cinética será:
Perceba que estamos convertendo de para ali em cima.
Passo 4
Como não há forças externas, podemos dizer que:
Cortando os
Resposta
Exercícios de Livros Relacionados
Resolva o Problema 13.68 considerando o coeficiente de atrito cinético entre o pacote e a inclinação é 0,2.
Um motor iça uma caixa de 60kg a uma velocidade constante até uma altura de h= 5m em 2s. Se a potencia indicada do motor é 3,2 kW, determine a eficiência do motor.
A caixa tem massa de 150 kg e repousa em uma superfície para a qual os coeficientes de atrito estático e cinético são μ F = 0.3 e μ k = 0.2 , respectivamente. Se o motor M fornece uma força no cabo F
Um satélite artificial que se desloca em uma órbita eliptica tem uma velocidade de 25000k m / h a uma altitude de 2200m no ponto A . Determine sua velocidade v B no ponto B onde a altitude é 2500k m .
O cursor de 0,6k g é liberado a partir do repouso em A e desliza para baixo na guia parabólica lisa (que está localizada em um plano vertical) sob a influência do seu próprio peso e da mola de constan