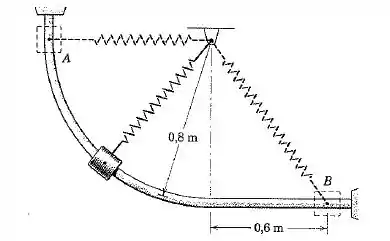
A mola tem um comprimento não esticado de e uma rigidez de . O Cursos de e a mola conectada são liberados a partir do repouso em e se deslocam no plano vertical. Calcule a velocidade do cursos quando este atinge na ausência de atrito.
Passo 1
Vamos usar, novamente:
Nesse caso, temos uma energia potencial e uma energia elástica. Assim;
Passo 2
Nesse problema, não existe a atuação de uma força externa, assim:
Podemos dizer, então:
Onde
A equação que escrevemos também pode ser escrita por:
Passo 3
A velocidade inicial é nula. Assim:
Considerando a altura inicial, altura em , igual a zero, podemos dizer que a variação de energia potencial gravitacional é negativa:
Perceba que a altura é o raio do ¼ de circunferência.
E a variação de energia potencial elástica?
Vamos ver.
Passo 4
Como:
Onde é o alongamento da mola, devemos calcular
Para os dois casos, o comprimento não esticado da mola vale
Em
E em
Bom, em você vai ter que calcular o comprimento de através do triângulo retângulo da figura. Assim:
Assim:
Então:
Passo 5
Assim:
Resolvendo: