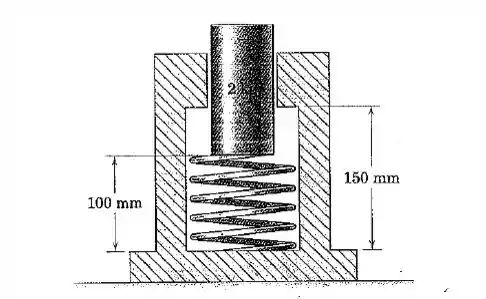
O êmbolo de é liberado a partir do repouso na posição mostrada onde a mola de rigidez foi comprimida para a metade do seu comprimento sem deformação de . Calcule a altura máxima acima da posição inicial alcançada pelo âmbolo.
Passo 1
Podemos aplicar:
Porém, não existe força externa aplicada, assim:
Então:
Passo 2
No início e no final o êmbolo se encontra em repouso, assim:
Então:
Passo 3
Assim:
Só que:
Resposta
Exercícios de Livros Relacionados
Resolva o Problema 13.68 considerando o coeficiente de atrito cinético entre o pacote e a inclinação é 0,2.
Um motor iça uma caixa de 60kg a uma velocidade constante até uma altura de h= 5m em 2s. Se a potencia indicada do motor é 3,2 kW, determine a eficiência do motor.
A caixa tem massa de 150 kg e repousa em uma superfície para a qual os coeficientes de atrito estático e cinético são μ F = 0.3 e μ k = 0.2 , respectivamente. Se o motor M fornece uma força no cabo F
Um satélite artificial que se desloca em uma órbita eliptica tem uma velocidade de 25000k m / h a uma altitude de 2200m no ponto A . Determine sua velocidade v B no ponto B onde a altitude é 2500k m .
O cursor de 0,6k g é liberado a partir do repouso em A e desliza para baixo na guia parabólica lisa (que está localizada em um plano vertical) sob a influência do seu próprio peso e da mola de constan