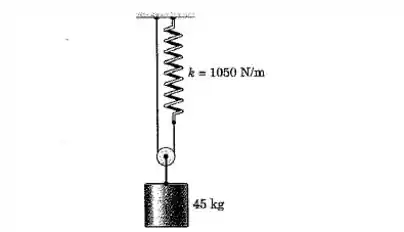
O sistema é liberado a partir do repouso com a mola inicialmente esticada em . Calcule a velocidade do cilindro após este ter caído . A mola tem uma rigidez de . Despreze a massa da pequena polia.
Passo 1
Vamos usar:
Como estamos lidando apenas com forças elásticas e gravitacionais:
Assim:
Passo 2
Assim:
Botamos um sinal de menos no último termo pois o enunciado disse que a massa “desceu”. Em outras palavras, a altura do ponto inicial é e a altura do ponto final é negativa.
Pelo enunciado, . Assim:
Temos:
Passo 3
Assim:
Resolvendo: