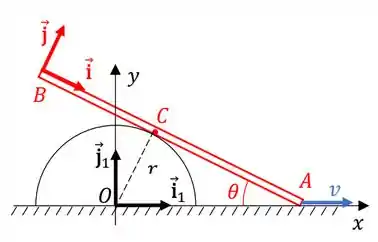
02) Conforme mostrado na figura, a barra se move no plano mantendo contato permanente com a semicircunferência de centro e raio e com o eixo horizontal . Admita-se, ainda, que a extremidade da barra se mova com velocidade ( constante). Expressando os resultados na base ligada à barra, determine para o instante em que :
a) As componentes segundo as direções (nesta ordem) da velocidade do ponto de contato barra.
b) A velocidade angular da barra .
c) A aceleração angular da barra
d) As componentes nas direções (nesta ordem) da aceleração do ponto barra.
Passo 1
Faaala pessoal, tudo tranquilo?
a) Nessa questão temos uma barra que se movimenta mantendo sempre um ponto de contato com uma semicircunferência. O enunciado mostra dois pares de eixos na estrutura, e .
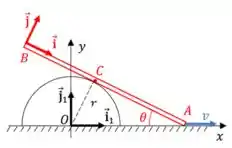
Além disso, também é dado que .
Beleza! Pra começar a resolução, devemos calcular a velocidade vetorial do ponto , no instante em que , usando os eixos . Mas como é que podemos fazer isso só com essas poucas informações?

Então galera, tem uma ideia de vínculo que é bem repetitiva nessas questões de movimento de barras e vale muito a pena a gente ter bem guardada na memória.
É que se uma barra está se movimentando, a velocidade de qualquer ponto da barra na direção do seu eixo precisa ser a mesma. Se isso não acontecesse, é como se a barra estivesse se descolando, bizarro né?!
Então, pensando no ponto e no ponto , lembrando que a barra está na direção temos:
Como o produto escalar representa a projeção de um vetor em uma determinada direção, podemos dizer que:
Massa! Daí, escrevendo segundo os eixos , temos:
Pô, então ainda falta descobrirmos essa componente . Tem um detalhezinho que passa quase despercebido no enunciado, mas dá pra tirar uma equação dele, sabe qual é?

O enunciado fala que a barra se move mantendo contato permanente com a semicircunferência. Imagina agora que o ponto de contato possua componente de velocidade em , então com certeza ela perderia o contato né? Por isso, a gente pode afirmar que:
Daí, finalizamos esse primeiro item com:
Prontinho 😉
Passo 2
b) Nesse item precisamos determinar a velocidade angular da barra .
Até agora a gente só sabe quanto vale e , certo?! Será que tem alguma equação que envolva essas duas variáveis junto com a velocidade angular?

Simmm! É a equação da velocidade em um movimento plano geral. Como o ponto é um contato permanente com a semicircunferência, é como se o ponto da barra estivesse rotacionando em relação a ele. Assim, temos:
Sabemos que , tomando as projeções de nas direções e , podemos escrever:
Além disso, pelo , retângulo em , podemos escrever:
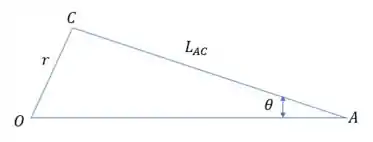
Assim, vem:
Massa, igualando as partes escalares temos:
Excelente! Da segunda equação, podemos fazer:
Usando , vem:
Eaí, entenderam direitinho?
Passo 3
c) Nesse item devemos calcular a aceleração angular da barra .
No item anterior encontramos que:
Mas a aceleração angular é simplesmente , assim derivando essa expressão temos:
Só dando uma manipulada, temos um resultado um pouco mais bonito:
Como , temos:
Substituindo e
Muito bom, galera! Agora falta só mais um item.
Passo 4
d) Nesse item devemos determinar a aceleração do ponto . Agora que estamos no final, é só seguir o fluxo e continuar nas equações do movimento plano geral, bora usar a da aceleração então:
Como a velocidade no ponto é constante, e substituindo temos:
Substituindo e , temos:
Fazendo , vem:
Ufaaa! Terminamos mais uma questão 😊
Até a próxima, pessoal!
Resposta
a)
b)
c)
d)