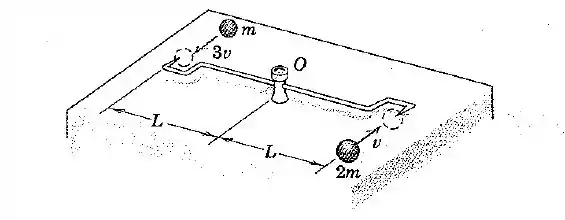
As pequenas esferas, que possuem as massas e velocidades iniciais indicadas na figura, atingem e tornam-se presas às extremidades pontudas da haste, que é livremente articulada em e está inicialmente em repouso. Determine a velocidade angular do conjunto após o impacto. Despreze a massa da haste.
Passo 1
Os momentos iniciais são:
E:
Passo 2
Após a colisão, o conjunto se comportará como um corpo só:
Assim, por conservação de momento angular( já que não há torques externos):
Resposta
Exercícios de Livros Relacionados
O fenômeno de “tropeço” de um veículo é investigado aqui. O veículo utilitário esportivo está deslizando para o lado com velocidade v 1 e sem velocidade angular quando atinge um pequeno meio-fio. Assu
O barco-bombeiro descarrega dois jatos de água do mar, cada um com vazão de 0,25m 3 / s a uma velocidade de saída de 50m / s . Determine a tração desenvolvida na corrente da âncora, necessária para se
O corpo rígido (placa) tem uma massa m e gira com uma velocidade angular ω em relação a um eixo passando pelo ponto fixo O. Demonstre que os momentos de todas as partículas compondo o corpo podem ser
Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo liberado de uma posição arbitrária com uma velocidade inicial arbitrária não pode passar mais de uma vez pela sua posição de equilí
O bloco mostrado na figura é abaixado em 30 mm da sua posiçãode equilíbrio e então liberado. Sabendo que depois de 10 ciclos odeslocamento máximo do bloco é de 12,5 mm, determine (a) o fatorde amortec