03) No sistema mostrado na figura a barra , de massa e comprimento , está articulada no ponto ao disco de massa e raio . O sistema está inicialmente em repouso, com a barra na posição vertical e com a reta que passa por e inclinada em um ângulo em relação à horizontal. Para o instante imediatamente após a liberação do sistema, determine:
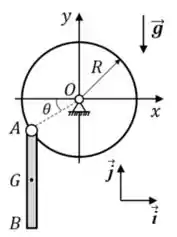
a) O vetor aceleração angular da barra.
b) A aceleração do centro de massa da barra.
c) O vetor aceleração angular do disco.
d) A força que a barra aplica no disco pela articulação do ponto .
Passo 1
Eaí pessoal, tudo bom com vocês?
Essa questão é bem complicadinha, porque tem pouquíssimas informações e muitaaas variáveis.
Em casos como esse, temos que ir recorrendo a todas as equações que conhecemos. No caso, é legal estruturar o pensamento nessa ordem:
- Equações da cinemática (aceleração do movimento plano geral)
- Teorema da quantidade de momento angular
- Teorema da Resultante
Tanto faz escrever primeiro o TQMA ou o Teorema da resultante, em geral quando você usa um também é necessário usar o outro.
Mas beleza! Agora que sabemos isso, bora pras contas!
Passo 2
Começando pela equação da aceleração no movimento plano geral, temos:
Para a barra:
Como , e imediatamente após a liberação , temos:
Beleza! Vê que agora já temos variáveis: e .
Então bora escrever a equação da aceleração de em relação ao centro do disco:
Usando que o ponto é fixo, que imediatamente após a liberação do movimento, , e que , vem:
Substituindo em , temos:
Muito bom! Já usamos a parte das equações cinemáticas.
Passo 3
Vamos agora pro teorema da quantidade de momento angular. Lembrando que esse teorema fala:
Nesse caso, para a barra usando o próprio polo , teremos:
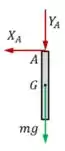
Sendo a reação horizontal no apoio , , e , temos:
Aplicando o mesmo teorema, mas agora para polo do disco, vem:
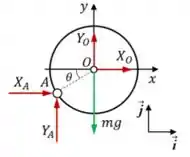
Sendo e as reações horizontal e vertical, respectivamente, em , e , o momento de inércia do disco, temos:
Logo:
Show! Até agora temos equações e variáveis:
Então precisamos de mais duas equações.
Passo 4
Pra conseguir essas duas equações, vamos usar a nossa última ferramenta: O teorema da resultante.
Então, para a barra, temos:
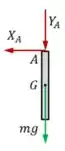
Daí, da equação , temos:
Substituindo e igualando as partes escalares, temos:
Massa!
Bora olhar pro disco agora:
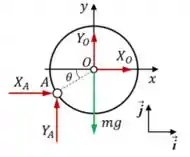
Se aplicarmos o teorema da resultante também para ele, ganharemos duas equações escalares, mas à custo de adicionar duas novas variáveis: e .
Então não vale a pena, porque nos itens desse exercício essas variáveis não foram pedidas.
Show! Bora agora resolver esse sisteminha (que de pequeno não tem nada haha).
Passo 5
Temos as seguintes equações:
Só de olhar já dá preguiça, né? Hahaha

Mas vamo simbora!
De , temos:
De substituindo em , vem:
Substituindo esses novos valores de e em , vem:
Isolando , temos:
Agora voltando para as equações das outras variáveis em função de :
Em :
Substituindo o valor de em , temos:
Pra finalizar essa questão, de , temos:
Ufaaaa! Esse sistema deu um trabalho hein galera!
Mas vencemos!!! Espero que vocês tenham entendido bem direitinho, até a próxima galera 😉
Resposta
a)
b)
c)
d)