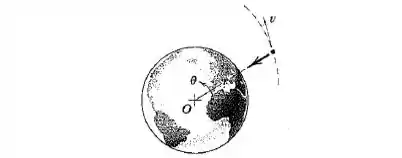
A única força atuando sobre um satélite da Terra que se desloca fora da atmosfera terreste é a atração gravitacional radial. O momento desta força é nulo em torno do centro da Terra tomado como um ponto fixo. Prove que permanece constante durante o movimento do satélite.
Passo 1
Podemos dizer que:
Onde:
Lembrando que:
Passo 2
Bom, beleza, mas quais são os momentos atuantes na partícula? Bom, como a força gravitacional é radial( aponta diretamente pro centro da terra), ela é perpendicular à velocidade do corpo.
Sendo assim, os torques são nulos:
Assim:
Assim:
O que isso significa? Se algo tem derivada nula, essa coisa é uma constante: