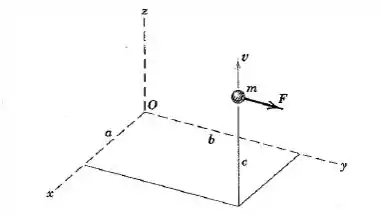
Em um dado instante, a partícula de massa tem a posição e velocidade mostradas na figura, e sofre a ação da força . Determine sua quantidade de movimento angular em torno do ponto e a taxa de variação no tempo dessa quantidade de movimento angular.
Passo 1
Vamos usar os nossos conhecimentos vetoriais lá de trás agora:
Onde:
E:
Assim:
Passo 2
Sabemos que:
E:
Resposta
Exercícios de Livros Relacionados
O fenômeno de “tropeço” de um veículo é investigado aqui. O veículo utilitário esportivo está deslizando para o lado com velocidade v 1 e sem velocidade angular quando atinge um pequeno meio-fio. Assu
O barco-bombeiro descarrega dois jatos de água do mar, cada um com vazão de 0,25m 3 / s a uma velocidade de saída de 50m / s . Determine a tração desenvolvida na corrente da âncora, necessária para se
O corpo rígido (placa) tem uma massa m e gira com uma velocidade angular ω em relação a um eixo passando pelo ponto fixo O. Demonstre que os momentos de todas as partículas compondo o corpo podem ser
Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo liberado de uma posição arbitrária com uma velocidade inicial arbitrária não pode passar mais de uma vez pela sua posição de equilí
O bloco mostrado na figura é abaixado em 30 mm da sua posiçãode equilíbrio e então liberado. Sabendo que depois de 10 ciclos odeslocamento máximo do bloco é de 12,5 mm, determine (a) o fatorde amortec