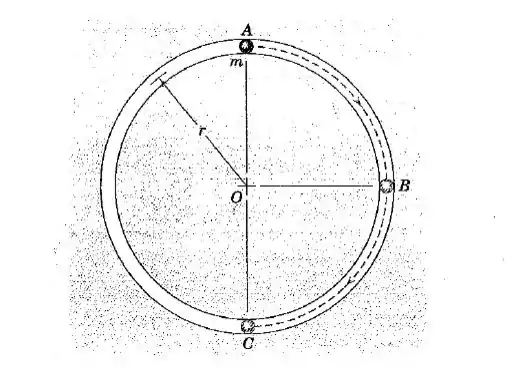
A partícula de massa é suavemente empurrada a partir da posição de equilíbrio e posteriormente desliza ao longo da trajetória circular lisa que se situa num plano vertical. Determine o módulo da sua quantidade de movimento angular em torno do ponto quando ela passa (a) o ponto e (b) o ponto . Em cada caso, determine a taxa de variação no tempo de .
.
Passo 1
a)
Para achar a velocidade no ponto , basta a gente aplicar a equação de Torriceli:
Onde:
Assim, o momento angular é dado por:
Vamos achar a taxa de variação do momento angular derivando isso em relação ao tempo, considerando que é uma função do tempo:
Passo 2
b)
Para achar a velocidade em , devemos fazer a mesma coisa:
Assim:
E derivando:
Ué? Por quê zero?
Simples: A força que está gerando a variação de momento angular é a força peso.
Sendo assim, quando a partícula passa pelo ponto , a força da gravidade, sendo vertical, não afeta o seu deslocamento, que é horizontal.