01) Um carretel de massa , de centro e raios (externo) e (interno) está articulado a uma barra de massa e comprimento , conforme indicado na figura. Mediante a aplicação de uma força (constante) a um cabo inextensível e de massa desprezível enrolado ao carretel, faz-se com que este role sem deslizar sobre um plano horizontal, arrastando consigo a barra . A polia de centro tem massa desprezível e o coeficiente de atrito entre as superfícies da barra e do plano horizontal é . é o ponto de contato do carretel com o plano horizontal. O momento de inércia do carretel em relação ao eixo é dado: . Pede-se:
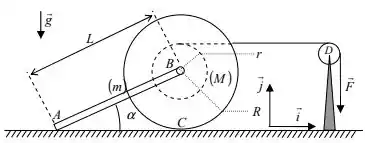
a) desenhar os diagramas de corpo livre do carretel e da barra;
b) determinar o momento de inércia do carretel em relação ao eixo ;
c) expressar as acelerações do baricentro da barra e do baricentro do carretel em função da aceleração angular do carretel;
d) escrever as equações dos teoremas do movimento do baricentro (TMB) e do momento da quantidade de movimento (TMQM ou TQMA, se se utilizar a terminologia ‘Teorema da Quantidade de Movimento Angular) para o carretel e para a barra.
Passo 1
Eaí gente bonita, tudo bom com vocês?
Nessa questão temos um carretel, com uma barra articulada, em uma de suas extremidades, no seu centro. A esse carretel passa-se um fio em sua região interna e traciona-se esse fio com uma força , gerando o movimento do conjunto.
a) Pra começar, devemos desenhar os diagramas de corpo livre do carretel e da barra.
O bizu pra desenhar DCL é sempre começar identificando as forças que agem no corpo.
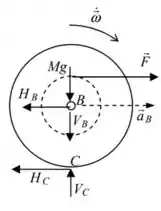
Iniciando pelo nosso carretel, temos a força do fio, o Peso agindo em , as reações em e em da articulação em . No ponto de contato , como é falado que o disco rola sem deslizar também há uma força de atrito, além da normal de contato. Daí, podemos desenhar:
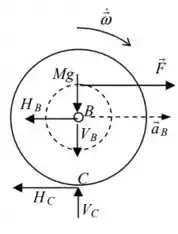
Muito bomm!
Pensando na barra , temos também as reações da articulação em (e aqui pelo equilíbrio do nó B, essas reações são iguais a e mas com sentido oposto ao desenhado no DCL do disco).
Além disso, também atua o Peso da barra no seu centro , e as reações de contato da barra com a superfície. Logo:
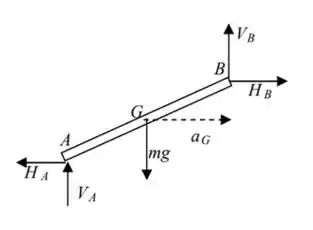
Bouaaa!
Passo 2
b) Devemos determinar o momento de inércia do carretel em relação ao eixo .
Beleza! O enunciado até nos falou o momento de inércia em relação ao centro do carretel, . Mas, como fazemos pra calcular o momento de inércia em relação a outro ponto?

Hahaha! Temos que usar o Teorema dos Eixos paralelos pessoal. Basicamente, ele diz que:
Como a distância entre e é justamente o raio , e , vem:
Prontinho 😊
Passo 3
c) Aqui devemos determinar a aceleração do baricentro da barra, ou seja, do ponto e do baricentro do carretel, ou seja, do ponto , em função da aceleração angular do carretel, , Sacaram?
Vamos começar pelo carretel! Beleza, sabemos a velocidade angular dele vale , mas o que podemos usar pra encontrar a velocidade do ponto ?

Nesses problemas de carretel (ou disco) a gente sempre ter que ficar ligado no rolamento que tá acontecendo.
Se vier uma informação tipo “o carretel rola sem deslizar” , que é o caso dessa questão, já podemos afirmar que a velocidade do ponto de contato é nula e que, ainda mais, esse ponto é um Centro instantâneo de rotação (CIR).
Portanto:
Como ele também é um CIR no instante considerado, é como se todos os pontos do carretel (inclusive ) estivessem rotacionando em volta dele. Daí:
Daí, derivando em relação ao tempo, temos:
Show!! Pensando na barra, temos um vínculo geométrico interessante.
Como a barra está articulada ao ponto , e o único movimento que ela realiza é o de translação (devido justamente à translação do carretel), ela deve transladar com a mesma aceleração de translação do carretel, ou seja, .
Logo:
Bouaaa!
Passo 4
d) Pra finalizar, vem a parte mais trabalhosa ☹
Devemos escrever as expressões do TMB e do TQMA para o carretel e para a barra.
Vamos começar aplicando o TMB para a barra:
O TMB é basicamente a lei de Newton considerando que toda a massa do corpo se concentra no baricentro. Daí, temos:
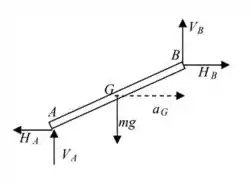
Lembrando que, como é uma força de atrito, vale
Aplicando o TMB para o carretel, teremos:
Perfeito! Vamos pensar agora no TQMA.
Para a barra , como ela não está rotacionando temos . Daí, escolhendo como polo, vem:
Top! Pra finalizar, escrevendo o TQMA com polo em , temos:
Prontinho! Temos então um sistema de equações e variáveis .
É isso aí galera! Espero que vocês tenham entendido bem direitinho, até a próxima 😊

Resposta
a) Resolução no texto.
b)
c)
d) Resolução no texto.