Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Impulso e Quantidade de Movimento Angular

Ver Teoria
Exercício 101234567891112

Enunciado

USP, Mecânica, P2-2017, Questão 02

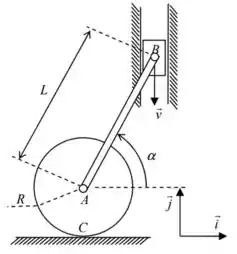
02) No mecanismo da figura ao lado, um disco de raio R , articulado em seu centro A a uma barra A B de comprimento L , rola sem escorregar sobre um plano horizontal fixo. A extremidade B da barra está articulada a um bloco que desliza sobre uma guia vertical com velocidade - v j → constante. Para o instante considerado na figura, pede-se:

a) o CIR da barra A B ;

b) a velocidade angular da barra A B ;

c) a velocidade do ponto A ;

d) a velocidade angular do disco;

e) a aceleração angular da barra A B ;

f) a aceleração do ponto A ;

Passo 1

Eaí pessoal, como vocês estãoo??

Bora matar mais uma questãozinha de mec 😉

Nesse exercício, temos um disco apoiado sobre uma superfície e preso à barra A B , que por sua vez está presa a um bloco que desliza em uma guia vertical. É dado que a velocidade do bloco é constante e vale - v j → .   A lém disso o disco está sempre apoiado sobre a superfície, de modo que a velocidade do seu centro, A , vale - v A i → .

a) Pra começar a questão, devemos encontrar o CIR da barra A B .

O CIR é o centro instantâneo de rotação, ele é o ponto que, no instante analisado, pode ser considerado como um centro para o movimento de rotação de qualquer ponto do corpo. Mas, como podemos fazer pra encontrar esse ponto?

Então, pra encontrar o CIR basta conhecermos a direção da velocidade de dois pontos distintos do corpo. Para cada uma dessas direções, traçamos uma reta perpendicular. O ponto de intersecção das retas é o CIR.

Nesse caso, como conhecemos a direção das velocidades de A e B , vamos ter:

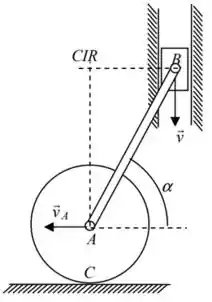
Prontinho 😊

Passo 2

b) Devemos determinar a velocidade angular da barra A B .

Lembra do que falamos antes sobre o CIR? Ele é um ponto que, no instante analisado, pode-se afirmar que qualquer outro ponto do corpo está rotacionando.

Massa né? Bora usar essa informação então. Tomando o ponto B , por exemplo. Podemos afirmar que:

v → B =   ω → A B × ( B - C I R )

Tomando apenas o módulo, como o CIR já é posicionado na direção perpendicular à velocidade, temos:

v B = ω A B r B , C I R

Pegaram a ideia?!

Mas, nós sabemos que:

v B =   v

Além disso, pelo triângulo A B ( C I R ) , podemos afirmar que:

r B , C I R = L c o s α

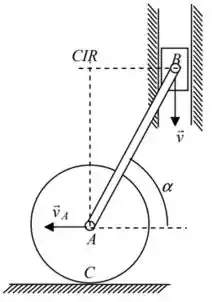
Portanto:

v =   ω A B L c o s α

∴ ω A B = v L c o s α

Bouaaaa galera!

Passo 3

c) Aqui devemos determinar a velocidade do centro A do disco.

Como havíamos falado antes, já que o disco se movimenta sempre apoiado na superfície, sabemos que:

v → A = - v A i →

O problema é: como determinar v A ?

A resposta pra isso é vínculo geométrico.

Pô, mas que danado de vínculo geométrico acontece nessa questão né?!

É que a barra que liga o bloco B ao disco é inextensível. Isso significa que as componentes da velocidade de qualquer ponto da barra na direção da mesma são todas iguais, sacaram?

Vamos usar os pontos A e B :

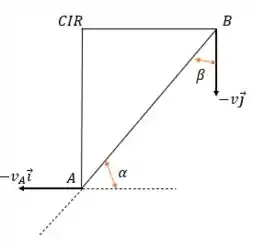
Daí, tomando as componentes na direção de A B , temos:

v A A B =   v A ⋅ c o s ⁡ ( α )

v B A B = v ⋅ c o s ⁡ ( β )

Só que β = 90 - α , assim:

v B A B = v ⋅ s e n ( α )

Igualando, temos:

v A ⋅ cos ⁡ α = v ⋅ s e n α

∴ v A = v ⋅ t g ( α )

Escrevendo vetorialmente, lembrando que a direção de v A é - i → , temos:

v → A = ( - v t g α ) i →

Aeee, prontinho. Essa dica do vínculo geométrico é bem legal né?

Passo 4

d) Aqui devemos calcular a velocidade angular do disco.

Galera, sempre que a questão pede pra calcular a velocidade angular do disco, temos que voltar lá no enunciado e verificar se tem uma informação crucial: “o disco rola sem escorregar.”

Essa informação é fundamental, porque significa que o ponto de contato do disco com a superfície é também um CIR.

Massa! Nessa questão, temos então o ponto C como um centro instantâneo de rotação para o disco. Logo, podemos escrever:

v A = ω d R

Como:

v A = v ⋅ t g α

Vem:

ω d = v ⋅ t g α R  

Prontinho, viram como saiu rápido desse jeito? É isso 😊

Passo 5

e) Estamos perto do final pessoal, bora dar o gás.

Precisamos calcular a aceleração angular da barra A B . Mas, qual que é a relação cinemática entre a velocidade e a aceleração angular mesmo?

É a relação da derivada, lembram?

ω ˙ A B = d ω A B d t

Como já calculamos anteriormente ω A B , essa expressão é perfeita. Bora lá!

ω ˙ A B = d d t v L c o s α

Retirando a constante v / L , ficamos com:

ω ˙ A B = v L ⋅ d d t 1 c o s α

Agora é só derivar, usando a regra da cadeira:

d c o s α - 1 d t =   - 1 ⋅ c o s α - 2 ⋅ ( - s e n α ) ⋅ d α d t

Mas,

d α d t = ω A B

Juntando tudo, temos:

ω ˙ A B = v s e n α L c o s 2 α ⋅ ω A B

⇒   ω ˙ A B = v s e n α L c o s 2 α ⋅ v L c o s α

ω ˙ A B = v 2 s e n α L 2 cos 3 ⁡ α  

Bouaaa galera! É isso aí!

Passo 6

f) Pra finalizar, vamos determinar a aceleração do ponto A .

Como já sabemos a aceleração e velocidade angular da barra A B , podemos usar a nossa fórmula do movimento pano geral:

a → A = a → B + ω → ˙ A B × A - B - ω A B 2 A - B

Como é falado no enunciado, v é constante. Assim:

a → B = 0

Além disso,

A - B = - L c o s α i → - L s e n α j →

Substituindo, temos:

a → A = v 2 s e n α L 2 cos 3 ⁡ α k → × - L c o s α i → - L s e n α j → - v L c o s α 2 ⋅ - L c o s α i → - L s e n α j →

⇒ a → A =   v 2 s e n α L cos 3 ⁡ α - c o s α j → + s e n α i → - v 2 L c o s 2 α ( - c o s α i → - s e n α j → )

a → A = v 2 L s e n 2 α cos 3 ⁡ α + 1 c o s α i → + v 2 L - s e n α c o s α cos 3 ⁡ α + s e n α cos 2 ⁡ α j →

Logo:

a → A = v 2 L c o s 3 α i →

Prontinho!! É isso aí galera, conseguiram entender bem?

Valeeeu, até a próxima 😉

Resposta

a) Resolução no texto.

b)

ω A B = v L c o s α

c) v → A = ( - v t g α ) i →

d) ω d = v ⋅ t g α R  

e) ω ˙ A B = v 2 s e n α L 2 cos 3 ⁡ α  

f) a → A = v 2 L c o s 3 α i →

Exercícios de Livros Relacionados

O fenômeno de “tropeço” de um veículo é investigado aqui. O veículo utilitário esportivo está deslizando para o lado com velocidade v 1 e sem velocidade angular quando atinge um pequeno meio-fio. Assu
O barco-bombeiro descarrega dois jatos de água do mar, cada um com vazão de 0,25m 3 / s a uma velocidade de saída de 50m / s . Determine a tração desenvolvida na corrente da âncora, necessária para se
O corpo rígido (placa) tem uma massa m e gira com uma velocidade angular ω em relação a um eixo passando pelo ponto fixo O. Demonstre que os momentos de todas as partículas compondo o corpo podem ser
Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo liberado de uma posição arbitrária com uma velocidade inicial arbitrária não pode passar mais de uma vez pela sua posição de equilí
O bloco mostrado na figura é abaixado em 30 mm da sua posiçãode equilíbrio e então liberado. Sabendo que depois de 10 ciclos odeslocamento máximo do bloco é de 12,5 mm, determine (a) o fatorde amortec