Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Medidas de Centralidade e Dispersão para V.A. Discreta

Ver Teoria
Exercício 12345678

Enunciado

Considere o lançamento de três moedas. Se ocorre o evento CCC, dizemos que temos uma sequência, ao passo que se ocorre o evento CRC temos três sequencias. Defina a v.a. X = número de caras obtidas e Y = número de sequências, isso para cada resultado possível. Assim, X C R R = 1 e Y C R R = 2 . Obtenha as distribuições de X e Y. Calcule E(X), E(Y), Var (X) e Var (Y).

Passo 1

Vamos lá então!

Primeira coisa que temos que fazer é: Escrever a distribuição de probabilidade tanto da v.a. X quanto da v.a. Y certo?

Pra isso temos que listar os eventos:

R R R ,   R R C ,   R C R ,   C R R ,   R C C ,   C R C ,   C C R ,   C C C

Esse aí é o nosso espaço amostral Ω .

Passo 2

Agora vamos entender quem é a v.a. X: número de caras obtidas e analisar os eventos:

1º evento: RRR → X = 0

P X = 0 = P R R R = 1 2 3 = 1 8

2º Evento: RRC → X = 1

P R R C = 1 2 3

Note que o 2º evento = 3º evento = 4º evento → Temos duas coroas e apenas uma cara? Ou seja, eles são as permutações possíveis certo? Então podemos falar que:

P X = 1 = 3 ! 2 ! . 1 2 3 = 3 8

5º evento: RCC → X = 2

P R C C = 1 2 3 = 1 8

Note que teremos um caso parecido com o evento 2. Note que o:

5º evento = 6º evento = 7º evento

Ou seja, temos nesses três casos uma coroa e duas caras. Esses casos são a permutações possíveis, então podemos falar que:

P X = 2 = 3 ! 2 ! 1 2 3 = 3 8

8º evento: CCC → X = 3

P X = 3 = P C C C = 1 2 3

Assim, podemos montar a tabela de distribuição de X:

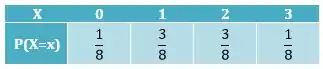
Passo 3

A partir disso podemos calcular E(x) e Var(x)

E x = ∑ i = 1 n x i . p ( x i )

E x = 0 ×   1 8 + 1 × 3 8 + 2 × 3 8 + 3 × 1 8 = 1,5

V a r x = ∑ i = 1 n [ x i - E X ] 2 × p i    

V a r x = - 1,5 2 × 1 8 + - 0,5 2 × 3 8 + 0,5 2 × 3 8 + 1,5 2 × 1 8 = 0,75

Passo 4

Agora vamos fazer o mesmo passo a passo para a v.a. Y: número de sequências

1º evento: RRR → Y = 1

P R R R = 1 2 3 = 1 8

2º Evento: RRC → Y = 2

P R R C = 1 2 3

3º Evento: RCR → Y = 3

P R C R = 1 2 3 = 1 8

4º Evento: CRR → Y = 2

P C R R = 1 2 3 = 1 8

5º evento: RCC → Y = 2

P R C C = 1 2 3 = 1 8

6º Evento: CRC → Y = 3

P C R C = 1 2 3 = 1 8  

7º Evento: CCR → Y = 2

P C C R = 1 2 3 = 1 8  

8º evento: CCC → Y = 1

P C C C = 1 2 3 = 1 8

Montando a tabela de distribuição de Y:

Passo 5

A partir disso podemos calcular E(y) e Var(y)

E Y = ∑ i = 1 n y i . p ( y i )

E Y = 1 ×   2 8 + 2 × 4 8 + 3 × 2 8 = 2

V a r Y = ∑ i = 1 n [ y i - E Y ] 2 × p i    

V a r Y = - 1 2 × 2 8 + 0 × 4 8 + 1 2 × 2 8 = 0,5

Resposta

E X = 1,5   ; V a r X = 0,75

E Y = 2 ; V a r Y = 0,5

Exercícios de Livros Relacionados

Árvores são sujeitas a diferentes níveis de atmosfera de dióxido de carbono com 6% das árvores em uma condição de crescimento mínimo a 350 partes por milhão (ppm) de C O 2 , 10% a 450 ppm (crescimento
Determine a média da variável aleatória T que representa o total de três moedas no Exercício 3.25.
A distribuição de probabilidade de X, o número de imperfeições por dez metros de um tecido sintético em rolos contínuos de largura igual, é dada no exercício 3.13 comoDetermine o número médio de imper
Determine a média e a variância da variável aleatória do Exercício 3-15.
Determine a médica e avariada da variável aleatória do Exercício 3-19.