Os funcionários de uma certa empresa, , , e ganham 1, 2, 2 e 4 salários mínimos respectivamente. Retiram-se amostras com reposição de 2 indivíduos e, mede-se o salário médio da amostra retirada. Calcule a média, o desvio padrão e o coeficiente de variação do salário médio amostral
Passo 1
Bom, vamos fazer que nem o exercício pede.
Montar todas as possíveis amostrar com 2 indivíduo, com reposição, o que significa que pode ter duas vezes o mesmo indivíduo. E ir medindo o salário médio de cada amostra.
Vou montar uma tabela marota!
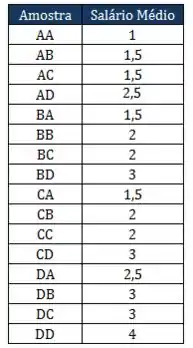
O salário médio é só somar o salário dos dois indivíduos de cada amostra e dividir por 2.
Passo 2
Se é a v.a. que representa o salário médio das amostras possíveis.
A gente consegue perceber que é uma v.a. discreta que pode assumir valores específicos, no caso: 1,0; 1,5; 2,0; 2,5; 3,0; 4,0.
Podemos montar uma tabela com a distribuição de probabilidades de cada um desses possíveis valores de .
Essa tabela vai nos ajudar a calcular o que precisamos.
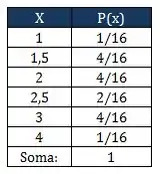
Passo 3
Pra calcular a média, ou esperança, vamos usar a fórmula:
Passo 4
Para a variância, vamos usar:
Passo 5
Agora podemos calcular o desvio padrão:
Passo 6
Pra fechar, o coeficiente de variação.