Determine as reações nos apoios e ; em seguida, trace o diagrama de momento fletor. Considere constante.
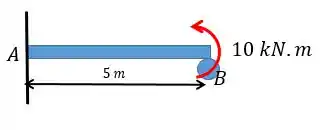
Passo 1
Faaala, galerinha!! Vamos resolver um exercício de vigas e eixos estaticamente indeterminados uhullll!!
O mais importante nesse problema é entender que ele não pode ser resolvido apenas pelas equações da estática porque é um problema hiperestático (tem um engaste e um apoio), então vamos utilizar a equação da linha elástica também, belezinha?
Então vamos começar fazendo o diagrama de corpo livre para entender como as reações são nesta questão e achar 3 equações. Depois a gente vai utilizar a equação da linha elástica como a nossa 4ª equação.
Então partiu!
Passo 2
Vamos começar fazendo o diagrama de corpo livre:
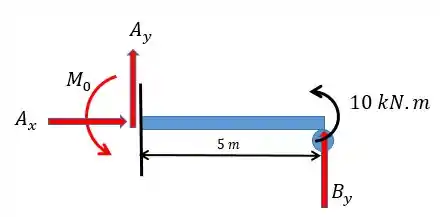
Observe que existem 4 reações e por isso que precisamos de 4 equações também. De qualquer forma vamos escrever as equações da estática para ver o que temos:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica, que é a parte mais legal da questão!

Boa que usou meme!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Onde é a equação do momento fletor. Então a gente precisa saber como o momento fletor se comporta nessa viga. Nós vamos fazer isso pelo método convencional das seções, belezinha?
Então fazendo um corte nessa viga vamos ter:
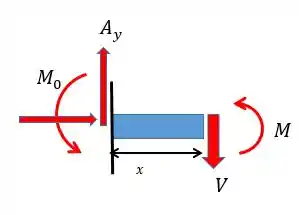
Pessoal, como queremos apenas o momento fletor então a gente parte direto para a equação do somatório dos momentos. Além disso para não precisar calcular o valor da força cortante vamos considerar o ponto de aplicação bem no corte:
Pronto! Acabamos de achar a equação do momento fletor!
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos integrar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
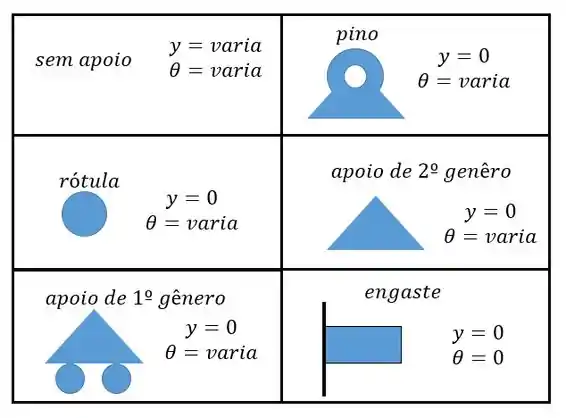
Então nós vamos ter as seguintes condições de contorno.
No engaste:
Na rótula:
Perceba que na rótula a viga está livre para rotacionar!
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
obs: Perceba que vamos utilizar a equação da angulação () e não a da deflexão (). Lembre também que
Essa é a nossa 4ª equação!! Agora é só voltar nas equações do passo 2 e resolver o sistema!
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Substituindo na 3ª equação:
Portanto vamos ter:
Passo 7
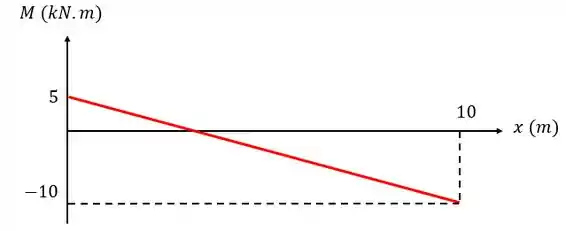
O problema também pediu para traçarmos o diagrama do momento fletor né? Se a gente já tem a equação, que foi achada no passo 3:
Substituindo os valores:
No diagrama vai ficar da forma:
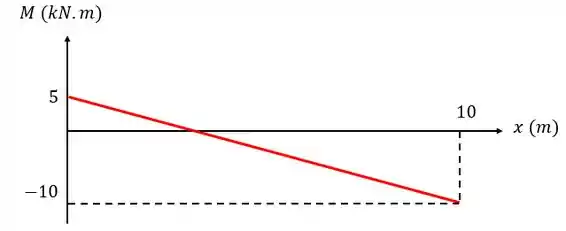
Resposta
Reações:
Diagrama: