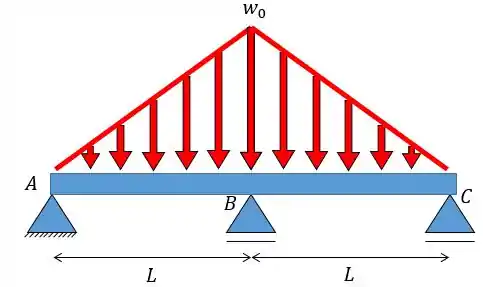
Determine as reações nos apoios e a seguir trace os diagramas de força cortante e momento. é constante.
Passo 1
Fala aí, galerinha!! Essa questão nos fornece uma viga apoiada em dois roletes e e num pino . Além disso, a viga possui um carregamento triangular e nos é pedido que achemos as reações dos apoios e os diagramas de força cortante e momento fletor.
Se montarmos o diagrama de corpo livre vamos ter o seguinte:
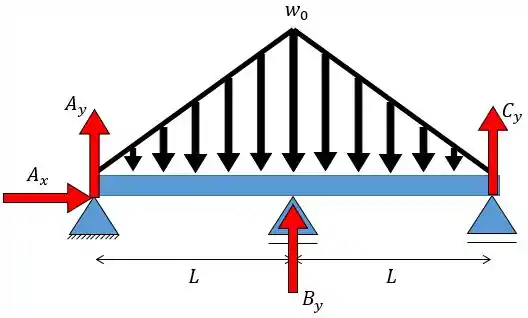
Primeiro é importante ressaltar que temos 4 forças de reação e por isso trata-se de um viga estaticamente indeterminada. Consequentemente, vamos ter de utilizar a equação da linha elástica como na nossa quarta equação. Caso não lembre a equação é dada por:
Então partiu resolver!
Passo 2
Nós já fizemos o diagrama de corpo livre e agora vamos utilizar as três equações das estática para determinar as três primeira equações:
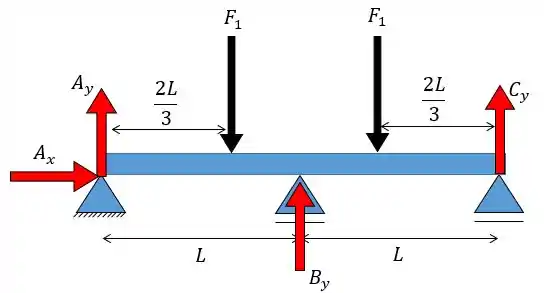
Perceba que o carregamento triangular foi dividido em dois carregamentos, também triangulares, e simétricos a qual cada um exerce uma força de valor . Onde cada força tem o valor de:
Utilizando as três equações vamos ter:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica. Essa é a parte mais crucial da questão!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Então a gente precisa da equação do momento fletor . Para tal vamos fazer um corte e obter:
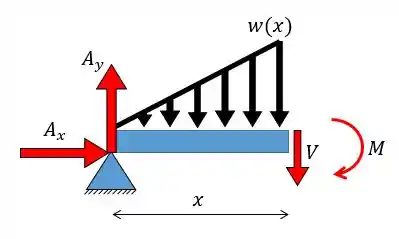
Agora temos de achar a equação que define o carregamento. A gente sabe que quandi o carregamento também vale zero e quando o carregamento vale . Como trata-se de uma variação linear então vamos ter:
Show! Agora é só aplicar o somatório dos momentos exatamente no ponto do corte (fazemos isso para não precisar calcular a força cortante). Considerando o sentido anti-horário positivo:
Lembrando que a força concentrada vale a metade do carregamento máximo vezes o comprimento:
E atua numa distância de do ponto , sendo assim:
Logo, a equação do momento fleotr pode ser dada por:
Prontinho, temos nossa função do momento fletor!
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez.
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
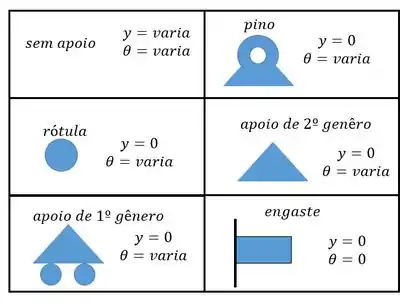
Então nós vamos ter as seguintes condições de contorno.
No ponto :
No ponto
No ponto :
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
Reorganizando nós temos:
Perceberam que agora temos mais uma equação? Essa equação junto com aquelas lá de cima vão fornecer os valores de .
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
A primeira parte do problema já foi, agora é só achar os diagramas!
Passo 7
Para achar os diagramas vamos colocar os dados que achamos na nossa viga:
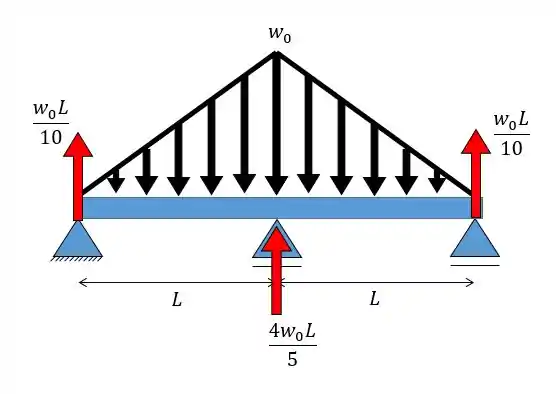
Assim, para fazer o diagrama da força cortante basta lembrar que quando temos um carregamento triangular a cortante é uma função de terceiro grau:
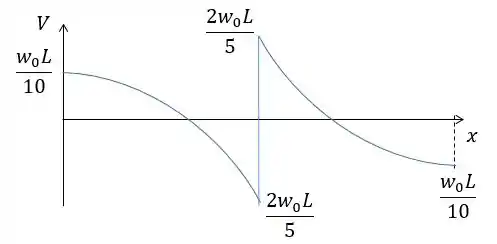
Passo 8
Para achar o diagrama da força cortante é só aplicar a equação que já achamos:
Agora sabemos o valor de :
Resposta
Reações:
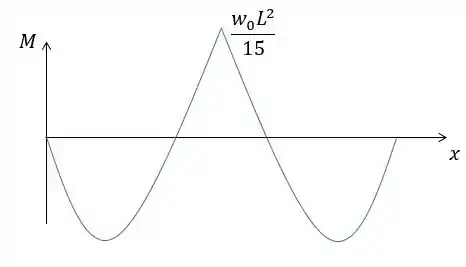
Diagrama da força cortante:
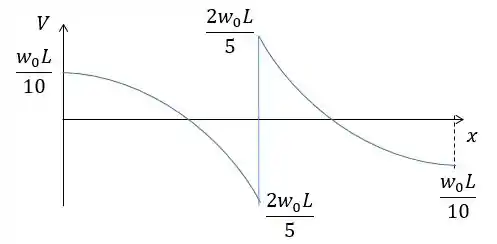
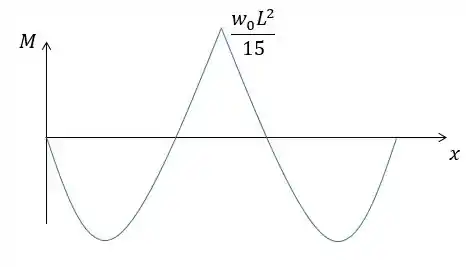
Diagrama do momento fletor: