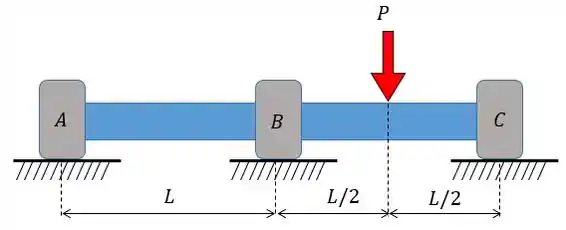
Determine as reações nos apoios e trace os diagramas de força cortante e momento fletor. é constante. O apoio é um mancal de encosto.
Passo 1
E aí, pessoal!! tranquilão com vocês? Olha essa questão de eixo que bacana, para a gente entender ela direitinho é importante notar que o mancal de enconsto vai ser o único que possui reação na horizontal beleza? Então se a gente fizer o diagrama de corpo livre vamos ter algo mais ou menos assim:
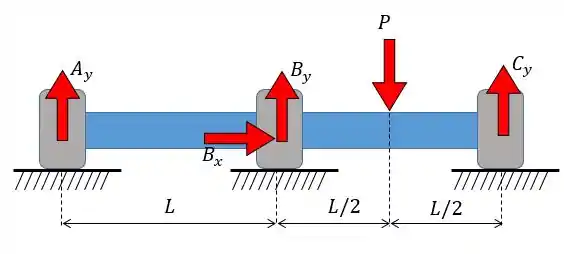
Aí perceba que temos 4 incógnitas e só temos 3 equações da estática para resolver esse tipo de problema. Então estamos falando de um eixo estaticamente indeterminado.
Para resolver problemas assim nós vamos utilizar nosso conceito de linha elástica porque assim vamos ter mais uma equação e conseguimos resolver o problema!!! Só pra lembrar que a linha elástica é dada por:
Então partiu resolver!
Passo 2
Nós já fizemos o diagrama de corpo livre e agora vamos utilizar as três equações das estática para determinar o máximo de relações possíveis:
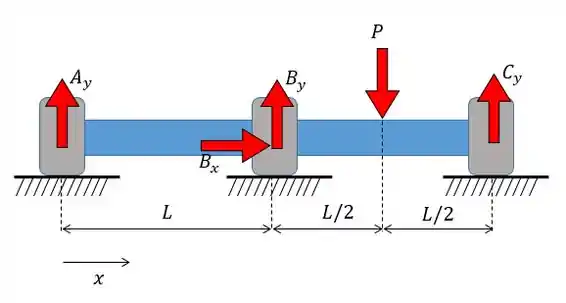
Utilizando as três equações vamos ter:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica. Essa é a parte mais crucial da questão!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Então a gente precisa da equação do momento fletor . Pessoal, aqui a gente meio que tem que utilizar funções de descontinuidade porque caso contrário iremos fazer muuuuita conta. Mas pode ficar tranquilo, vamos fazer juntos e ainda vou te dar uma tabelinha aqui pra te ajudar:
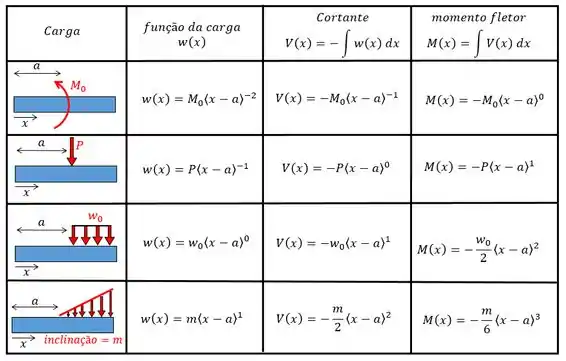
Como nesse problema temos apenas forças então todos os momentos serão da forma:
Vamos fazer devagarinho:
- Para a força em vamos ter:
- Para a força em vamos ter:
- Para a força vamos ter:
- Para a força em vamos ter:
Perceba que a força está no sentido positivo, logo o sinal do momento também é positivo. Além disso a força atua em .
obs: Como esse é o último termo a gente poderia ignorar, mas na real não faz diferença colocar ou não ok?
Então agora é só somar todos os termos:
Prontinho, temos nossa função do momento fletor escrita em termos de função de descontinuidade!
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez.
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
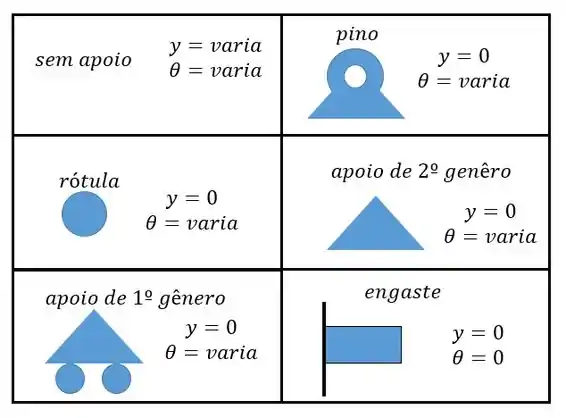
Então nós vamos ter as seguintes condições de contorno.
No ponto :
No ponto
No ponto :
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
Como podemos eliminar alguns termos e irá sobrar:
Substituindo
Como , novamente poderemos retirar alguns termos o obter:
Substituindo:
Agora a gente pode retirar o termo ou não tanto faz!! De qualquer maneira vai dar zero.
Substituindo então vamos ter:
Reorganizando nós temos:
Perceberam que agora temos mais uma equação? Essa equação junto com aquelas lá de cima vão fornecer os valores de .
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Passo 7
O problema também pediu para traçarmos os diagramas da força cortante e do momento fletor né? A equação do momento fletor a gente já tem:
Substituindo os valores:
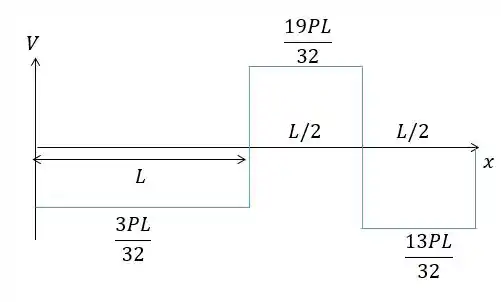
Ou podemos também jogar direto os valores das reações no eixo e obter o diagrama que vai ficar da forma:
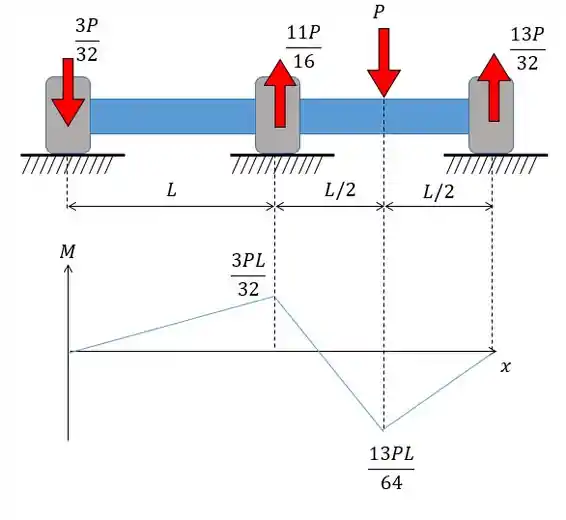
Passo 8
Para achar o diagrama da força cortante é só derivar o momento:
Derivando:
Da mesma forma podemos utilizar as reações direto no eixo e obter:
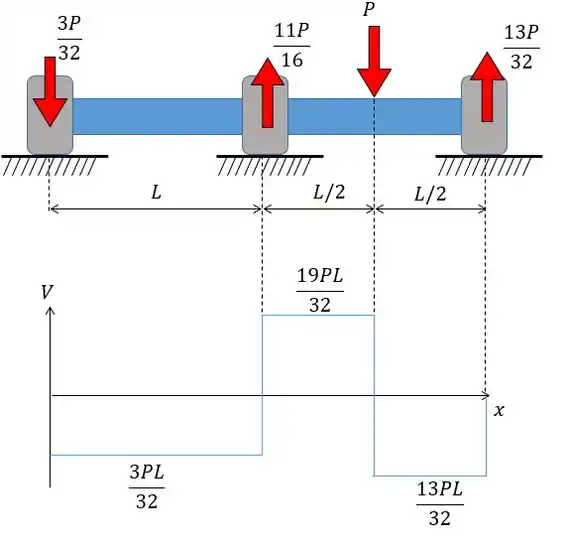
Resposta
Reações:
Diagrama do momento fletor:
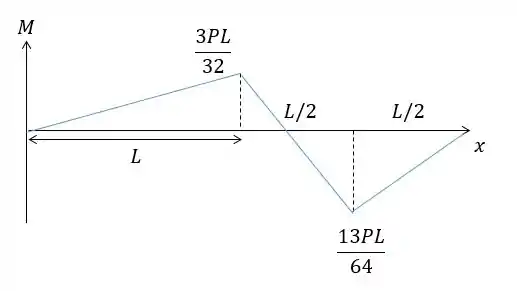
Diagrama da força cortante: