Determine a deflexão na extremidade da tira de aço . A rigidez da mola é . Considere que a barra tem de base.
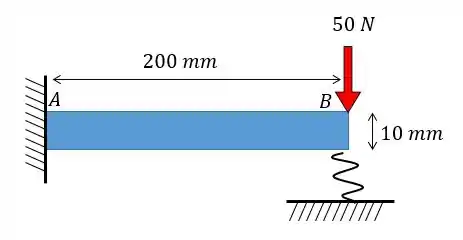
Passo 1
Vamo lá, galera, resolver mais uma questão aí!
A configuração desse problema é de uma barra engastada com uma força sendo aplicada na ponto, até aí suave. A questão é que existe uma mola também e essa mola, ao deformar, irá aplicar uma força oposta na barra.
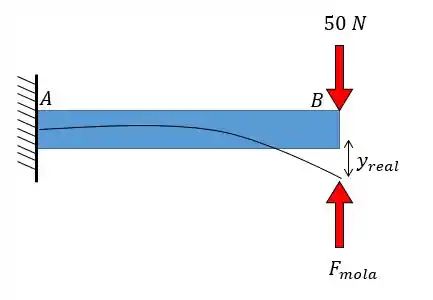
A grande sacação desse problema é calcular a deflexão real da barra devido a duas forças: da mola e da força .
Passo 2
A deflexão real da barra tem a seguinte equação:
Onde representa a deflexão causada pela força de e a deformação causada pela mola.
A gente pode achar a deflexão causada pela força de através da tabela e vamos encontrar:
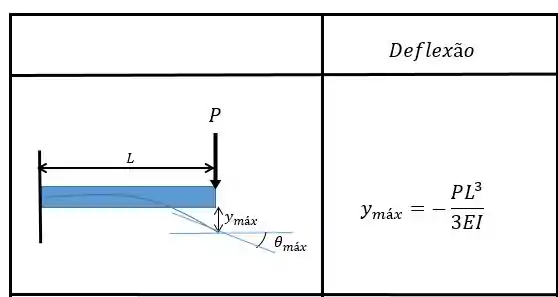
Passo 3
Já a deflexão causada pela mola depende da deformação que a mola sofre, lembra da força da mola?
Mas aqui que tá o pulo do gato. A deflexão real é a própria deformação da mola, então:
Como é uma força que atua na extremidade da barra então nós vamos ter:
Lembrando que o sinal está positivo porque a força aponta para cima.
Agora é só juntar as duas equações:
Fica mais fácil se colocarmos a força da mola em função de . Lembrando que a deformação da mola e para baixo, logo o fica negativo
Passo 4
Para resolver essa equação a gente precisa lembrar que o aço tem . Além disso, temos de lembrar do cálculo do momento de inércia:
Nós vamo ter também que o coeficiente da mola é:
Agora é só substituir
E a deflexão terá o mesmo valor e sentido para baixo: